01.递归

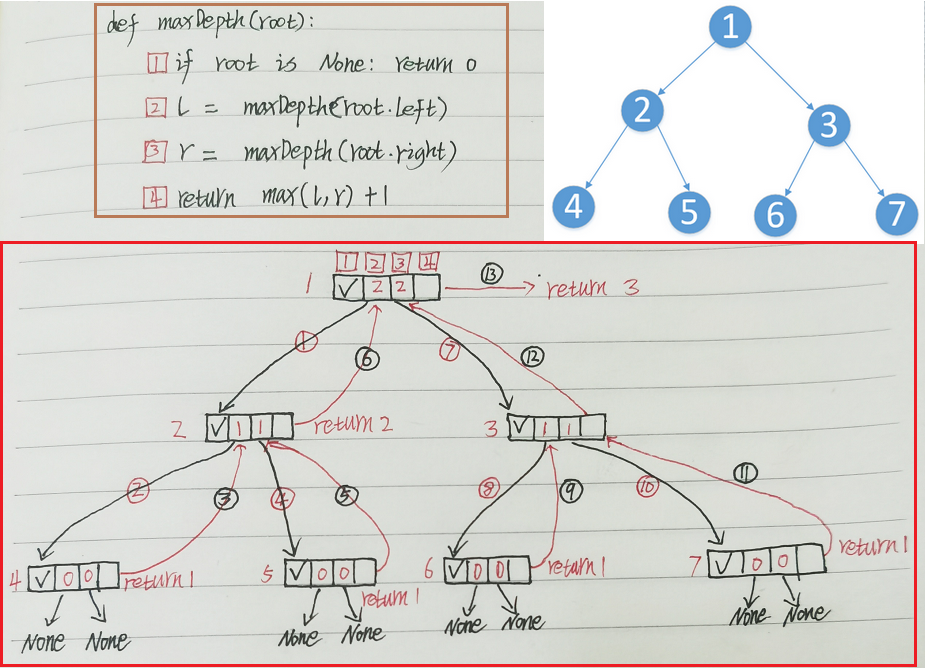
1、树高度

        1
       / \
      2   3
     / \ / \
    4  5 6  7

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def maxDepth(root):
    if root is None:
        return 0
    l = maxDepth(root.left)
    r = maxDepth(root.right)
    return max(l, r) + 1

if __name__ == '__main__':
    root = TreeNode(1,
                    left=TreeNode(2, TreeNode(4), TreeNode(5)),
                    right=TreeNode(3, TreeNode(6), TreeNode(7))
                    )
    print(maxDepth(root))  # 输出 3

2、递归分析

1）访问根节点1：

• root = TreeNode(1)，递归访问左子树 l = maxDepth(root.left)，进入节点 TreeNode(2)

2）递归到节点2：

• 递归访问左子树 l = maxDepth(root.left)，进入节点 TreeNode(4)

3）处理叶子节点4：

• 节点 TreeNode(4) 没有子节点，递归返回0，max(l, r) + 1 结果为 1，返回给节点 TreeNode(2)

4）处理节点5：

• 返回到节点 TreeNode(2)，递归访问右子树 r = maxDepth(root.right)，进入节点 TreeNode(5)
• 节点 TreeNode(5) 没有子节点，递归返回0，max(l, r) + 1 结果为 1，返回给节点 TreeNode(2)

5）计算节点2的深度：

• 节点 TreeNode(2) 左右子树深度 L=1，R=1，计算出深度 2，返回给根节点 TreeNode(1)

6）处理节点3：

• 返回到根节点 TreeNode(1)，递归访问右子树 r = maxDepth(root.right)，进入节点 TreeNode(3)

7）递归到节点6和7：

• 递归访问节点 TreeNode(3) 的左子树 TreeNode(6) 和右子树 TreeNode(7)，它们都没有子节点，递归返回 1

8）计算节点3的深度：

• 节点 TreeNode(3) 左右子树深度 L=1，R=1，计算出深度 2，返回给根节点 TreeNode(1)

9）计算根节点的深度：

• 根节点 TreeNode(1) 左右子树深度 L=2，R=2，最终计算出树的最大深度为 3

02.分治

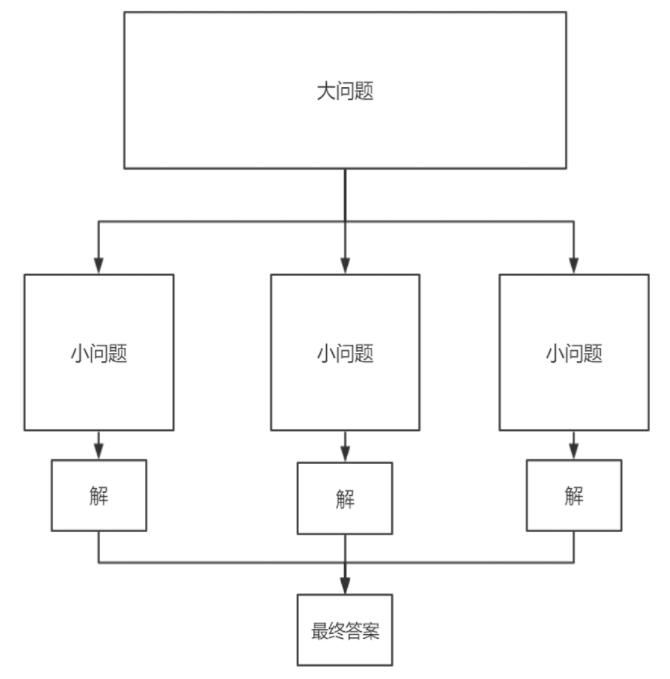
1、分治算法

• 分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题
• 求出子问题的解，就可得到原问题的解
• 分解（Divide）：
  • 将一个数组递归地分成两半，直到子数组的大小为1
  • 这时，数组被认为是已经排序的
• 解决（Conquer）：
  • 当子数组只有一个元素时，递归开始回溯，并逐步合并这些已排序的小数组
• 合并（Combine）：
  • 在合并的过程中，比较子数组的元素，将它们合并成一个更大的已排序数组

2、归并

def mergesort(arr):
    # 如果数组长度小于2，直接返回数组
    if len(arr) < 2:
        return arr
    
    # 计算中间位置，将数组分为左右两部分
    mid = len(arr) // 2
    left_half = mergesort(arr[:mid])
    right_half = mergesort(arr[mid:])
    
    # 合并排序后的左右两部分
    return merge(left_half, right_half)

def merge(left, right):
    result = []
    i = j = 0
    
    # 合并两个有序数组
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    
    # 添加剩余的左半部分元素
    result.extend(left[i:])
    # 添加剩余的右半部分元素
    result.extend(right[j:])
    
    return result

# 示例使用
arr = [10, 4, 6, 3, 8, 2, 5, 7]
sorted_arr = mergesort(arr)
print(sorted_arr)  # 输出: [2, 3, 4, 5, 6, 7, 8, 10]

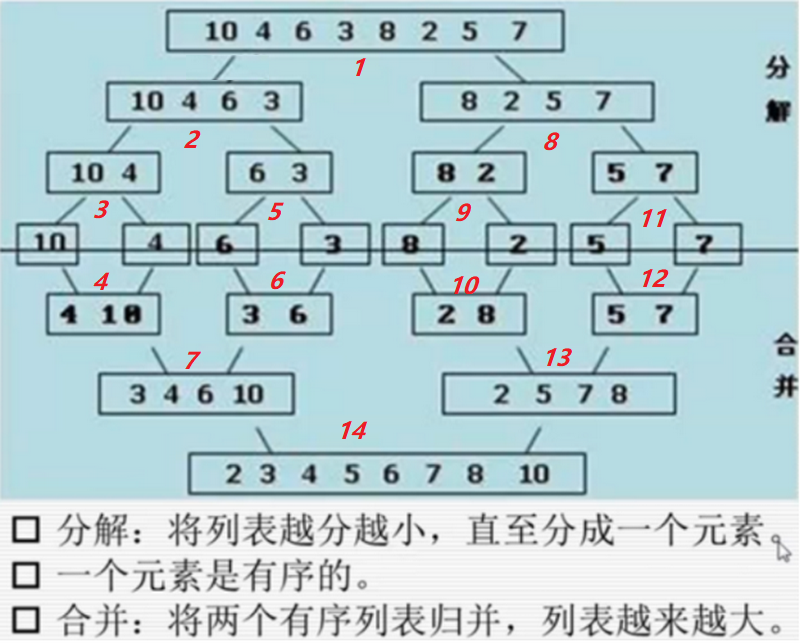
3、解析

第一步：分解

• 分成 [10, 4, 6, 3] 和 [8, 2, 5, 7]

第二步：递归分解左半部分 [10, 4, 6, 3]

• 分成 [10, 4] 和 [6, 3]

第三步：递归分解 [10, 4]

• 分成 [10] 和 [4]，因为每个子数组只有一个元素，递归达到最小单位，开始合并

第四步：合并 [10] 和 [4]

• [10] 和 [4] 合并为 [4, 10]，这时 [10, 4] 的合并完成

第五步：递归分解 [6, 3]

• 分成 [6] 和 [3]，然后合并 [6] 和 [3]，结果为 [3, 6]

第六步：合并 [4, 10] 和 [3, 6]

第七步：递归分解右半部分 [8, 2, 5, 7]

• 分成 [8, 2] 和 [5, 7]

第八步：递归分解 [8, 2]

• 分成 [8] 和 [2]，然后合并为 [2, 8]

第九步：递归分解 [5, 7]

• 分成 [5] 和 [7]，然后合并为 [5, 7]

第十步：合并 [2, 8] 和 [5, 7]

第十一步：合并左右两部分 [3, 4, 6, 10] 和 [2, 5, 7, 8]

03.双指针

• 双指针，顾名思义，就是利用两个指针去遍历数组
• 一个放首，一个放尾，同时向中间遍历，直到两个指针相交，完成遍历，时间复杂度也是O(n)

1、两数之和II

• 两数之和 II - 输入有序数组 (opens new window)

• 题目描述

  • 给定一个已按照 升序排列 的整数数组 numbers
  • 请你从数组中找出两个数满足相加之和等于目标数 target
  • 你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素

输入：numbers = [2,3,4], target = 6
输出：[1,3]
输入：numbers = [-1,0], target = -1
输出：[1,2]

• 解题思路
  • 初始时两个指针分别指向第一个元素位置和最后一个元素的位置
  • 每次计算两个指针指向的两个元素之和，并和目标值比较
  • 如果两个元素之和等于目标值，则发现了唯一解
  • 如果两个元素之和小于目标值，则将左侧指针右移一位
  • 如果两个元素之和大于目标值，则将右侧指针左移一位

def twoSum(numbers, target):
    low, high = 0, len(numbers) - 1
    while low < high:
        total = numbers[low] + numbers[high]
        if total == target:
            return [low + 1, high + 1]
        elif total < target:
            low += 1
        else:
            high -= 1
    return [-1, -1]

if __name__ == '__main__':
    numbers = [2,3,4]
    target = 6
    print( twoSum(numbers, target) )