 06.动态规划
06.动态规划
- 动态规划(DP)是一种通过分解问题、保存中间结果来避免重复计算的优化方法
- 动态规划算法将待求解问题拆分成一系列
相互交叠的子问题 - 通过递推关系定义各子问题的求解策略,并
随时记录子问题的解 - 最终获得原始问题的解,
避免了对交叠子问题的重复求解
# 01.线性 DP 模型
- 特点:通常用于求解一个数组或序列的最优解
- 状态定义:
dp[i]表示从数组nums开头到nums[i]这个位置,最长的严格递增子序列的长度 - 状态转移方程:
dp[i] = max(dp[i], dp[j] + 1)(条件nums[j] < nums[i]) - 初始状态:
dp数组初始为[1, 1, 1, 1, 1, 1, 1, 1],表示每个元素单独作为一个子序列的长度为1
# 1、最长递增子序列
- 300.最长递增子序列 (opens new window)
- 给你一个整数数组
nums,找到其中最长严格递增子序列的长度
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4
1
2
3
2
3
# 2、python
- 状态定义:
dp[i]表示从数组nums开头到nums[i]这个位置,最长的严格递增子序列的长度 - 状态转移方程:
dp[i] = max(dp[i], dp[j] + 1)(条件nums[j] < nums[i]) - 初始状态:
dp数组初始为[1, 1, 1, 1, 1, 1, 1, 1],表示每个元素单独作为一个子序列的长度为1 - 通过逐步更新
dp数组,最终dp变成[1, 1, 1, 2, 2, 3, 4, 4],因此最长递增子序列的长度为 4
class Solution:
def lengthOfLIS(self, nums):
dp = [1] * len(nums) # 初始化 每个元素单独作为一个子序列的长度为1
for i in range(1, len(nums)): # 每次都比较 0~i-1的值与 nums[i]比较
for j in range(i):
if nums[i] > nums[j]: # nums[i]更大 代表 可以接在 nums[j] 后面
dp[i] = max(dp[i], dp[j] + 1)
return max(dp) # 返回 dp 数组中的最大值,即为最长递增子序列的长度
print(Solution().lengthOfLIS([10, 9, 2, 5, 3, 7, 101, 18])) # 输出: 4
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
- 如何更新
dp[i]:- 我们想要找到
nums[i]之前的元素中所有比nums[i]小的元素nums[j](其中j < i) - 如果
nums[j] < nums[i],那么dp[i]可以更新为dp[i] = max(dp[i], dp[j] + 1) - 表示
nums[i]可以接在nums[j]后面(遍历0~i-1 多有数据即可知道接在哪里最长)
- 我们想要找到
# 02.双序列 DP 模型
- 特点:处理两个序列之间的关系,常用于求解序列匹配、编辑距离等问题
# 1、最长公共子序列
给定两个字符串
text1和text2,返回这两个字符串的最长 公共子序列 的长度如果不存在 公共子序列 ,返回
0由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0
1
2
3
4
5
6
7
2
3
4
5
6
7
# 2、python
状态定义:
dp[i][j]表示字符串text1的前i个字符和字符串text2的前j个字符的最长公共子序列的长度状态转移方程:
- 如果
text1[i-1] == text2[j-1],则dp[i][j] = dp[i-1][j-1] + 1,表示当前字符匹配,公共子序列长度加 1 - 如果
text1[i-1] != text2[j-1],则dp[i][j] = max(dp[i-1][j], dp[i][j-1]),表示字符不匹配,选择之前的较长子序列
- 如果
初始状态:
创建一个大小为
(m+1) x (n+1)的二维数组dp,其中所有元素初始化为0因为空字符串与任何字符串的最长公共子序列长度都是 0,这个数组用于存储子问题的解
- 时间复杂度:
O(m * n)- 空间复杂度:
O(m * n)二维数组来存储中间结果
def longestCommonSubsequence(text1, text2):
m, n = len(text1), len(text2)
# dp[i][j] 表示 text1 前 i 个字符和 text2 前 j 个字符的最长公共子序列的长度
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1): # i指针遍历 text1 字符串
for j in range(1, n + 1): # j指针遍历 text2 字符串
if text1[i - 1] == text2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1 # 如果当前字符相同,取前一状态(对角线)的值加 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) # 如果当前字符不同,取 dp[i-1][j] 和 dp[i][j-1] 中的最大值
return dp[m][n] # 最终结果位于 dp[m][n],即为最长公共子序列的长度
print(longestCommonSubsequence("abcde", "ace")) # 输出: 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 3、推演结果
下面是以
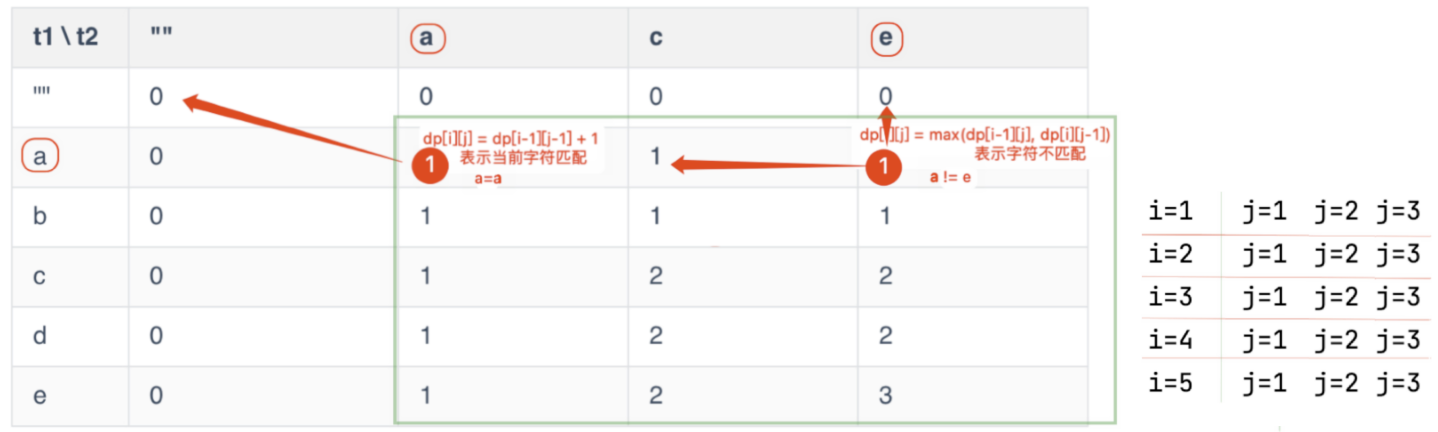
text1 = "abcde"和text2 = "ace"为例,按照类似格式展示dp数组的构建过程状态定义:
dp[i][j]表示字符串text1的前i个字符和字符串text2的前j个字符的最长公共子序列的长度状态转移方程:
- 如果
text1[i-1] == text2[j-1],则dp[i][j] = dp[i-1][j-1] + 1,表示当前字符匹配,公共子序列长度加 1 - 如果
text1[i-1] != text2[j-1],则dp[i][j] = max(dp[i-1][j], dp[i][j-1]),表示字符不匹配,选择之前的较长子序列
- 如果
初始状态:
dp[i][0] = 0和dp[0][j] = 0,因为空字符串与任何字符串的最长公共子序列长度都是 0
# 03.背包问题
- 有一个背包,其最大承重为
W,有n个物品,每个物品有一个重量w[i]和一个价值v[i]- 目标是选择一些物品放入背包中,使得背包中的物品总重量不超过
W,并且这些物品的总价值最大化
# 1、零钱兑换 最少硬币数
给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额计算并返回可以凑成总金额所需的
最少的硬币个数如果没有任何一种硬币组合能组成总金额,返回
-1你可以认为每种硬币的数量是无限的
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
输入:coins = [2], amount = 3
输出:-1
输入:coins = [1], amount = 0
输出:0
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# 2、python
状态定义:我们定义一个一维数组
dp,其中dp[i]表示凑成金额i所需的最少硬币个数状态转移方程:
dp[i] = min(dp[i], dp[i - coin] + 1)dp[i - coin]是前面的计算结果,代表金额i - coin最少用了多少硬币+1是再加上当前硬币coin,就变成了imin(dp[i], dp[i - coin] + 1)是找出最优解,确保dp[i]存的是最少的硬币数
初始状态:
[0, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]dp[i]表示 凑成金额i所需的最少硬币数dp[0] = 0(金额为 0,不需要硬币)- 其他
dp[i]初始化为一个不可能达到的值,通常设置为amount + 1(这里是12) - 确保
min(dp[i], dp[i - coin] + 1)能正确更新dp[i]
class Solution:
def coinChange(self, coins, amount):
# 初始化 dp 数组,长度为 amount + 1,所有值初始为 amount + 1(表示一个不可能达到的值)
dp = [amount + 1] * (amount + 1)
dp[0] = 0 # 当金额为 0 时,所需硬币数为 0
for i in range(1, amount + 1): # 遍历从 1 到 amount 的所有金额
for coin in coins: # 对于每个金额,遍历所有硬币面值
if i >= coin: # 硬币大于当前 i 位置索引不进入循环
dp[i] = min(dp[i], dp[i - coin] + 1) # 更新 dp[i],取最小值
# 如果 dp[amount] 仍然为初始值,说明无法凑出这个金额,返回 -1
return dp[-1] if dp[-1] != amount + 1 else -1
print( Solution().coinChange([1, 2, 5], 11) ) # 输出: 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 3、推演结果
- 状态定义:我们定义一个一维数组
dp,其中dp[i]表示凑成金额i所需的最少硬币个数 - 状态转移方程:
dp[i] = min(dp[i], dp[i - coin] + 1)dp[i - coin]复用i - coin所在位置中计算的最小数量,加上当前硬币,就是当前硬币 i位置最小数量
- 初始状态:
[0, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]- 初始时所有金额都不可能被凑出,金额为
0时,不需要任何硬币
- 初始时所有金额都不可能被凑出,金额为
- 硬币:
[1, 2, 5]目标金额:11
金额 | dp[金额] | 硬币组合
-----|----------|------------
0 | 0 | []
1 | 1 | [1]
2 | 1 | [2]
3 | 2 | [1, 2]
4 | 2 | [2, 2]
5 | 1 | [5]
6 | 2 | [1, 5] 或 [1, 2, 2]
7 | 2 | [2, 5]
8 | 3 | [1, 2, 5] 或 [1, 1, 2, 2, 2]
9 | 3 | [2, 2, 5]
10 | 2 | [5, 5]
11 | 3 | [1, 5, 5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
金额:i = 2dp[2]初始化值为12
# 第 1 次迭代 (i = 1)
硬币 1:更新 dp[1] = min(dp[1], dp[1 - 1] + 1) => dp[1] = 1
结果:[0, 1, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
# i= 1小于硬币 2和5,所以 i >= coin 条件不成立
# 第 2 次迭代 (i = 2)
硬币 1:更新 dp[2] = min(dp[2], dp[2 - 1] + 1) => dp[2] = 2
硬币 2:更新 dp[2] = min(dp[2], dp[2 - 2] + 1) => dp[2] = 1
结果:[0, 1, 1, 12, 12, 12, 12, 12, 12, 12, 12, 12]
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# dp[i] = min(dp[i], dp[i - coin] + 1)
# dp[i - coin] 复用 i - coin 所在位置中计算的最小数量,加上当前硬币,就是当前硬币 i位置最小数量
1
2
2
上次更新: 2025/3/19 18:46:49
