01.数组

# `① 数组操作`

# 01.买卖股票的最佳时机

121.买卖股票的最佳时机 (opens new window)
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格
如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润
注意你不能在买入股票前卖出股票

输入: [7,4,6,3,1]
输出: 2

1
2

1、Python

有 买入（buy） 和 卖出（sell） 这两种状态
当天买的话意味着损失 -prices[i]，当天卖的话意味着增加 prices[i]，当天卖出总的收益就是 buy+prices[i]
所以我们只要考虑当天买和之前买哪个收益更高，当天卖和之前卖哪个收益更高
buy = max(buy, -price[i]) （注意：根据定义 buy 是负数）
sell = max(sell, prices[i] + buy)

def maxProfit(prices):
    if len(prices) <= 1:
        return 0
    buy = prices[0]  # 当天买的话意味着损失 -prices[i]
    sell = 0
    for i in prices:
        buy = min(buy, i)  # 当前买的价格 比 以前买入的大,就在当前节点买入
        sell = max(sell, i-buy)  # 卖的价钱 = 现在成交价格i - 购买价格buy
    return sell

print(maxProfit([7,4,6,3,1]))    # 2

1
2
3
4
5
6
7
8
9
10
11

2、Go

func maxProfit(prices []int) int {
	if len(prices) <= 1{
		return 0
	}
	buy := prices[0]  // 当天买的话意味着损失 -prices[i]
	sell := 0       // 初始化利润为0
	for _, price := range prices{
		if price < buy {  // 当前买的价格 比 以前买入的大,就在当前节点买入
			buy = price   // 卖的价钱 = 现在成交价格i - 购买价格buy
		}
		if price-buy > sell{  // 如果当前价格减卖的价格 大于记录的最大利润，就更新最大利润
			sell = price-buy
		}
	}
	return sell
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 02.买卖股票的最佳时机II

122.买卖股票的最佳时机II (opens new window)
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格
在每一天，你可以决定是否购买和/或出售股票你在任何时候最多只能持有一股股票
你也可以先购买，然后在同一天出售，返回 *你能获得的最大利润

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3
最大总利润为 4 + 3 = 7

1
2
3
4
5

1、Python

max_profit 初始化为 0，用于存储最大利润
我们从数组的第二天开始遍历 (i 从 1 开始)，检查当前价格是否高于前一天的价格
如果价格上涨 (prices[i] > prices[i - 1])，则将上涨的差值加入 max_profit 中
这样做相当于每天都买入并卖出股票，只要有利润就加上
最后返回 max_profit，即最大总利润

def maxProfit(prices):
    max_profit = 0
    for i in range(1, len(prices)):
        # 如果今天的价格高于昨天的价格，就在今天卖出，赚取差价
        if prices[i] > prices[i - 1]:
            max_profit += prices[i] - prices[i - 1]
    return max_profit

print(maxProfit([7, 1, 5, 3, 6, 4]))  # 输出：7

1
2
3
4
5
6
7
8
9

# 03.删除有序数组中重复项

26.删除有序数组中的重复项 (opens new window)
给你一个 非严格递增排列 的数组 nums ，请你** 原地 (opens new window)** 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度
元素的 相对顺序 应该保持一致，然后返回 nums 中唯一元素的个数

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2，不需要考虑数组中超出新长度后面的元素

1
2
3

1、Python

使用 count指针记录当前列表中无重复数字的长度
使用 i 指针遍历列表，如果相邻两个元素不相等，什么都不处理
如果相邻两个元素不相等，就将不重复的值放到 count指针位置
遍历完结果：

nums = [0, 0, 1, 1, 1, 2, 2 ,3, 3, 4]   # 原始列表
nums = [0, 1, 2, 3, 4, 2, 2, 3, 3, 4]   # 遍历后结果，count=5，遍历后取出 nums[5]，就是目标结果

1
2

def removeDulp(nums):
    count = 1
    for i in range(1, len(nums)):
        if nums[i] != nums[i - 1]:
            # 如果相邻两个元素不相等，就将 不重复的值放到 count指针位置
            nums[count] = nums[i]
            count += 1
    return count

print( removeDulp([0,0,1,1,1,2,2,3,3,4]) )  # 5, [0, 1, 2, 3, 4, 2, 2, 3, 3, 4]

1
2
3
4
5
6
7
8
9
10

# 04.2 删除有序数组中的重复项 II

80.删除有序数组中的重复项 II (opens new window)
给你一个有序数组 nums ，请你** 原地 (opens new window)** 删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度
不要使用额外的数组空间，你必须在 原地 (opens new window)修改输入数组 并在使用 O(1) 额外空间的条件下完成

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 不需要考虑数组中超出新长度后面的元素

1
2
3

1、Python

class Solution:
    def removeDuplicates(self, nums):
        if not nums:
            return 0
        slow = 2   # `slow` 用于记录结果数组的位置，允许元素最多出现两次

        for i in range(2, len(nums)):
            # 如果当前元素与 `slow - 2` 位置的元素不同，说明当前元素可以加入结果数组
            if nums[i] != nums[slow - 2]:
                nums[slow] = nums[i]  # 将当前元素放到 `slow` 位置
                slow += 1  # 移动 `slow` 指针，准备放置下一个元素
        return slow

1
2
3
4
5
6
7
8
9
10
11
12

# 05.找到所有数组中消失的数字

448.找到所有数组中消失的数字 (opens new window)
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的整型数组，数组中的元素一些出现了两次，另一些只出现一次
找到所有在 [1, n] 范围之间没有出现在数组中的数字
您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内

输入:
[4,3,2,7,8,2,3,1]
输出:
[5,6]

1
2
3
4

1、Python

利用索引标记：

我们遍历数组中的每个数字，并利用该数字（减 1 后）的索引位置将数组中对应的值标记为负数
例如，若当前数字为 4，则将 nums[3]（即索引 3 对应的元素）标记为负数这样，我们就可以知道数字 4 出现在数组中

找到未标记的索引：

遍历完成后，数组中那些正数位置的索引 + 1 就是缺失的数字，因为这些位置没有被标记为负数，说明对应的数字从未出现过

时间复杂度：

这个算法的时间复杂度为 O(n)，因为我们只需要遍历数组两次
空间复杂度为 O(1)，因为我们没有使用额外的空间（不计算返回结果的空间

def findNums(nums):
    n = len(nums)
    for num in nums:
        # 计算对应的索引位置（需要使用模运算避免数组越界）
        x = (num - 1) % n
        # 在该索引位置的值上增加n，以标记该数字出现过
        nums[x] += n
    
    # 找出数组中值未超过n的位置，这些位置对应的数字即为缺失的数字
    ret = [i + 1 for i, num in enumerate(nums) if num <= n]
    
    return ret

nums = [4, 3, 2, 7, 8, 2, 3, 1]
print(findNums(nums))  # 输出: [5, 6]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 06.缺失的第一个正数

41.缺失的第一个正数 (opens new window)
给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案

输入：nums = [3,4,-1,1]
输出：2
解释：1 在数组中，但 2 没有

1
2
3

1、Python

对于一个长度为 N 的数组，其中没有出现的最小正整数只能在 [1,N+1] 中
将 nums 数组本身当作哈希表来使用
遍历数组 nums，对于每个元素 nums[i]，尝试将它放到对应的位置，即 nums[nums[i] - 1]
在放置过程中，需要考虑以下条件：
- 忽略非正数和超过数组长度的数
- 如果目标位置已经放置了正确的数，则跳过，以避免无限循环
最终数组中第一个不符合条件的位置的索引加 1 就是缺失的最小正整数

class Solution:
    def firstMissingPositive(self, nums):
        n = len(nums)
        for i in range(n):
            # 尝试将 nums[i] 放到 nums[nums[i] - 1] 的位置上
            # eg: nums[i] = 3 应该放到 nums[2]位置上
            while 1 <= nums[i] <= n and  nums[i] !=  nums[nums[i] - 1]:
                nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
        for i in range(n):        # 寻找第一个 nums[i] != i + 1 的位置
            if nums[i] != i + 1:
                return i + 1
        return n + 1              # 如果所有位置都正确，则返回 n + 1

print( Solution().firstMissingPositive([11,1,3,4,5,6,7,8,9,10]) )
# 最终 nums=[1, 11, 3, 4, 5, 6, 7, 8, 9, 10]   缺失的最小正整数就是 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

推演: 对于一个长度为 N 的数组，其中没有出现的最小正整数只能在 [1,N+1] 中

# 初始数组 nums = [11, 1, 3, 4, 5, 6, 7, 8, 9, 10]
# i = 0 时
nums[0] = 11，因为 11 > 10（超出了数组的索引范围），我们不需要进行交换，直接进入下一个索引

# i = 1 时
nums[1] = 1，它应该放在索引 0 处（1-1=0），交换后得到 nums = [1, 11, 3, 4, 5, 6, 7, 8, 9, 10]
此时，nums[1] = 11，因为 11 > 10（超出了数组的索引范围），我们不需要进行交换，直接进入下一个索引

# i = 2 时
nums[2] = 3，它已经在正确的位置（索引 2，即 3-1=2），不需要进一步交换
# 最终的数组是 [1, 11, 3, 4, 5, 6, 7, 8, 9, 10]， 缺失的最小正整数就是 2

1
2
3
4
5
6
7
8
9
10
11

# 07.移动零

283.移动零 (opens new window)
给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

1
2

1、Python

我们创建两个指针i和j，第一次遍历的时候指针j用来记录当前有多少 "非0元素"
即遍历的时候每遇到一个非0元素就将其往数组左边挪
第一次遍历完后，j指针的下标就指向了最后一个非0元素下标
第二次遍历的时候，起始位置就从j开始到结束，将剩下的这段区域内的元素全部置为0

class Solution:
    def moveZeroes(self, nums):
        j = 0   # j指针记录非0的个数，只要是非0的统统都赋给nums[j]
        for i in range(len(nums)):
            if nums[i]:
                nums[j] = nums[i]
                j += 1
        for i in range(j,len(nums)):  # 二次遍历把末尾的元素都赋为0即可
            nums[i] = 0
        return nums

print( Solution().moveZeroes([0,1,0,3,12]) )  # [1, 3, 12, 0, 0]

1
2
3
4
5
6
7
8
9
10
11
12

# 08.两个数组的交集

349.两个数组的交集 (opens new window)

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]

1
2

1、Python

def disNum(nums1, nums2):
    _set = set(nums1)  # 将nums1转换成集合
    result = []

    for num in nums2:
        if num in _set:    # 如果nums2中元素在集合中
            result.append(num)
            _set.discard(num)   # 集合中去除刚刚已经添加的元素，避免重复解
    return result

1
2
3
4
5
6
7
8
9

# 09.两个数组的交集 II

350.两个数组的交集 II (opens new window)
给定两个数组，编写一个函数来计算它们的交集

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]
输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]

1
2
3
4

1、Python 字典方法

class Solution:
    def intersect(self, nums1, nums2):
        dic = {}   # 哈希表
        for num in nums1:
            dic[num] = dic.get(num, 0) + 1

        res = []
        for num in nums2:
            if dic.get(num, 0) > 0:
                res.append(num)
                dic[num] -= 1  # 使用一次就减少

        return res

1
2
3
4
5
6
7
8
9
10
11
12
13

# 10.加一

66.加一 (opens new window)
给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一

输入：digits = [1,2,3]
输出：[1,2,4]
输入：digits = [9,9,9]
输出：[1,0,0,0]

1
2
3
4

1、Python

class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        carry = 1  # 进位
        p = len(digits) - 1  # p指针从右侧开始
        while p >= 0:
            sum = digits[p] + carry
            digit = sum % 10  # 当前数字
            carry = sum // 10  # 进位
            digits[p] = digit
            p -= 1
        if carry == 1:
            digits = [1] + digits
        return digits

1
2
3
4
5
6
7
8
9
10
11
12
13

# 11.列表连续相同数据放一起

力扣删除了

将列表：# [1,2,2,3,4,4,5,6,6,6,7,8,2,2,2]
转换成：# [[1], [2, 2], [3], [4, 4], [5], [6, 6, 6], [7], [8], [2, 2, 2]]

1
2

1、Python

初始化 result 和 current_group：用于存储结果列表和当前正在处理的连续相同元素的分组
遍历原列表：逐个检查元素是否与当前分组的最后一个元素相同，相同则加入当前分组，不同则结束当前分组并开始新的分组
添加最后一个分组：在遍历结束后，将最后一个分组添加到结果列表中，确保所有元素都被处理

def group_eles(lst):
    if not lst:
        return []

    result = []  # 用于存储最终的结果
    current_group = [lst[0]]  # 初始化第一个分组，包含列表的第一个元素

    for i in range(1, len(lst)):
        if lst[i] == current_group[-1]:
            # 如果当前元素和当前分组的最后一个元素相同，则将其加入当前分组
            current_group.append(lst[i])
        else:
            # 如果当前元素和当前分组的最后一个元素不同，则将当前分组加入结果中
            result.append(current_group)
            # 开始一个新的分组
            current_group = [lst[i]]

    result.append(current_group)  # 添加最后一个分组到结果中
    return result

# 测试用例
lst = [1, 2, 2, 3, 4, 4, 5, 6, 6, 6, 7, 8, 2, 2, 2]
print(group_consecutive_elements(lst))  # 输出: [[1], [2, 2], [3], [4, 4], [5], [6, 6, 6], [7], [8], [2, 2, 2]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 12.下一个排列

31.下一个排列 (opens new window)
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列
从右往左找到第一个小于其右侧元素的数字，交换位置就是下一个排列
例如，arr = [1,2,3] 的下一个排列是 [1,3,2]
而 arr = [3,2,1] 的下一个排列是 [1,2,3]

1、Python

假设我们有一个数字序列 [1, 3, 5, 4, 2]，我们需要找到这个序列的下一个排列 –> [1, 4, 2, 3, 5]

1）步骤 1: 从右往左找到第一个小于其右侧元素的数字
- 2<4, 4<5, 5>3，左侧3小于右侧5，3 就是我们需要调整的元素，位置是 i = 1
2）步骤 2: 从右往左找到第一个比3大的元素并交换
- 2<3, 4>3, 4就是是第一个比 3 大的数字， 3 和 4 交换，序列变为 [1, 4, 5, 3, 2]
3）步骤 3: 反转交换位置后的右侧部分
- 交换位置4(i=1)，右侧部分为5, 3, 2 ，反转后的序列是 [1, 4, 2, 3, 5]（这个就是下一个排列）

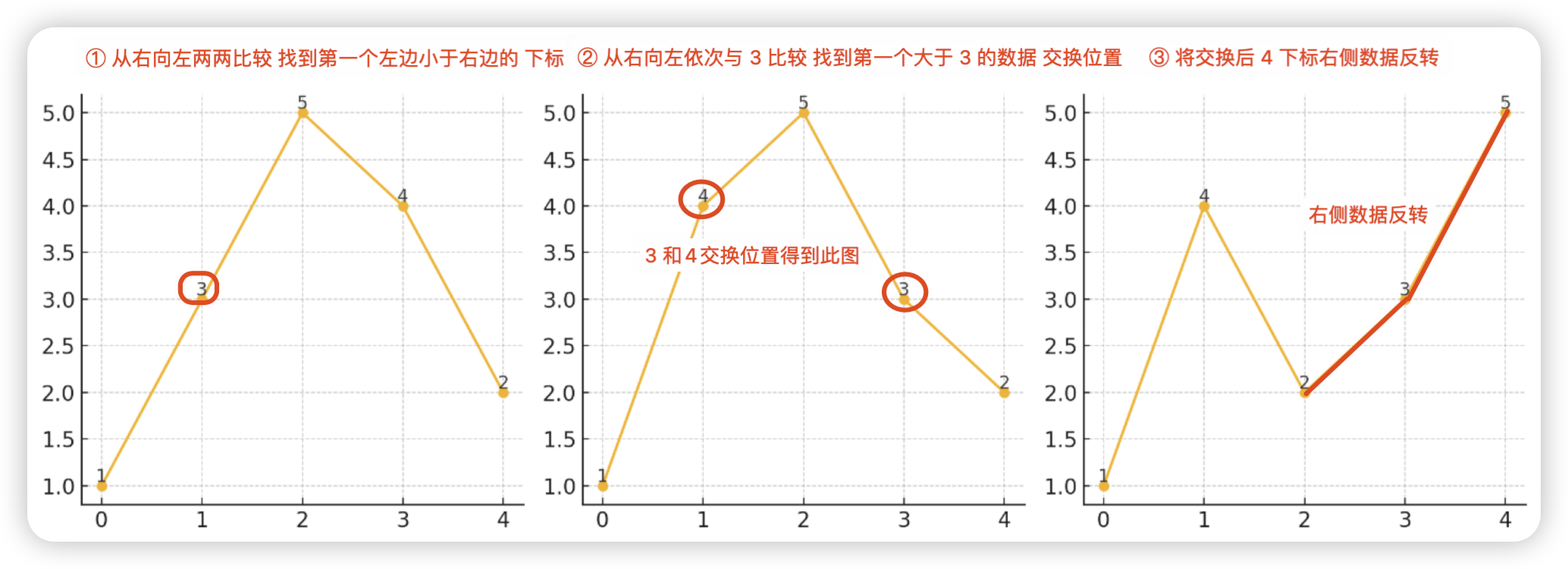
class Solution:
    def nextPermutation(self, nums):
        # 第一步：从右往左找到第一个小于其右侧元素的数字
        i = len(nums) - 2
        while i >= 0 and nums[i] >= nums[i + 1]:
            i -= 1

        if i >= 0:  # 如果找到这样的元素
            # 第二步：从右往左找到第一个大于 nums[i] 的数字
            j = len(nums) - 1
            while nums[j] <= nums[i]:  # 第一步中 i+1 肯定是，所以至少存在一个
                j -= 1

            nums[i], nums[j] = nums[j], nums[i] # 交换 nums[i] 和 nums[j]

        # 第三步：反转 i 索引后的所有元素
        l, r = i + 1, len(nums) - 1
        while l < r:
            nums[l], nums[r] = nums[r], nums[l]
            l += 1
            r -= 1
        print(nums)  # [1, 3, 2]


Solution().nextPermutation([1, 2, 3])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#

# ② 其他

# 13.柱状图中最大的矩形

84.柱状图中最大的矩形 (opens new window)
给定 n 个非负整数，用来表示柱状图中各个柱子的高度每个柱子彼此相邻，且宽度为 1
求在该柱状图中，能够勾勒出来的矩形的最大面积

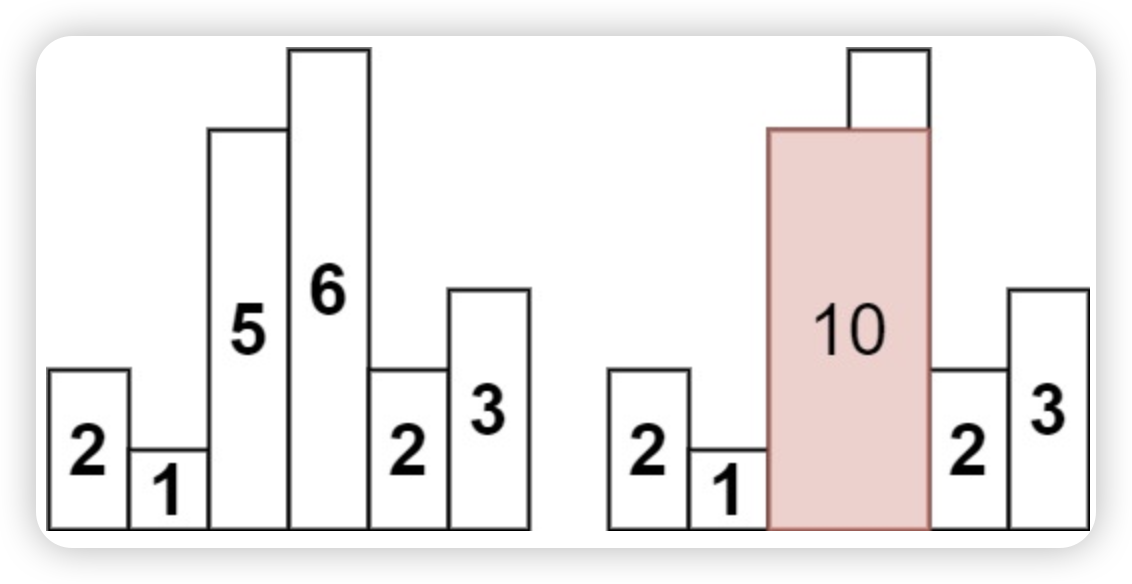
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10  #（5,6两个组成）

1
2
3

1、Python

末尾添加一个 0，保证所有柱子都能被正确弹出并计算面积
使用 enumerate() 遍历 heights，i 是索引，h 是高度
如果当前 h 大于等于 栈顶索引对应的高度，入栈（保持递增）
如果当前 h 小于栈顶索引对应的高度，说明右边界确定，计算矩形面积
- 弹出栈顶元素作为矩形高度 height
- 确定矩形宽度
  - 若 栈为空，说明弹出的柱子是最左端的柱子，宽度为 i
  - 若 栈不为空，则宽度 = i - stack[-1] - 1（两柱子之间的宽度）
- 计算面积 height * width 并更新 max_area

class Solution:
    def largestRectangleArea(self, heights):
        # 在 heights 末尾添加一个 0，确保所有柱子都会被计算
        heights.append(0)
        stack = []      # 维护一个单调递增栈，存储柱子的索引
        max_area = 0    # 记录最大矩形面积

        for i, h in enumerate(heights):
            # 当当前柱子的高度小于栈顶柱子的高度时，说明找到了右边界
            while stack and heights[stack[-1]] > h:
                height = heights[stack.pop()]  # 弹出栈顶元素，作为矩形的最小高度
                width = i if not stack else i - stack[-1] - 1  # 计算矩形的宽度
                max_area = max(max_area, height * width)  # 更新最大面积

            stack.append(i)   # 当前索引入栈（保持栈内高度递增

        return max_area

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 14.最长连续序列

128.最长连续序列 (opens new window)
给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度
请你设计并实现时间复杂度为 O(n) 的算法解决此问题

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]它的长度为 4

1
2
3

1、Python

将nums转换为 set集合
循环遍历集合中元素，判断当前元素是否是 序列起点（i-1不在集合中）
不断查找连续序列，直到i的下一个数不存在于数组中

class Solution:
    def longestConsecutive(self, nums):
        res = 0                              # 记录最长连续序列的长度
        set_ = set(nums)                     # 记录is中的所有数值
        for i in set_:
            if (i - 1) not in set_:          # 如果当前的数是一个连续序列的起点，统计这个连续序列的长度
                len_ = 1                     # 连续序列的长度，初始为1
                while (i + 1) in set_:
                    len_ += 1
                    i += 1                   # 不断查找连续序列，直到i的下一个数不存在于数组中
                res = max(res, len_)         # 更新最长连续序列长度
        return res

1
2
3
4
5
6
7
8
9
10
11
12

# 15.最大数

179.最大数 (opens new window)
给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数
**注意：**输出结果可能非常大，所以你需要返回一个字符串而不是整数

输入：nums = [3,30,34,5,9]
输出："9534330"

1
2

1、Python

通过自定义冒泡排序，两两相加比较，如果交换位置结果更大就交换位置

class Solution:
    def largestNumber(self, nums):
        def bubble_sort(nums):
            for i in range(len(nums)):
                for j in range(0, len(nums) - i - 1):
                    # nums[j]=3  nums[j + 1]=30   330 > 303 条件不成立，不交换
                    if nums[j] + nums[j + 1] < nums[j + 1] + nums[j]:
                        # 如果 nums[j] + nums[j+1] 小于 nums[j+1] + nums[j]，交换位置
                        nums[j], nums[j + 1] = nums[j + 1], nums[j]
        nums_str = list(map(str, nums))       # ['3', '30', '34', '5', '9']
        bubble_sort(nums_str)                 # ['9', '5', '34', '3', '30']
        result = ''.join(nums_str)            # 拼接排序后的数字
        if result[0] == '0':                  # 特殊情况处理：如果结果的第一个字符是 '0'，则说明所有数字都是 0
            return '0'
        return result

print( Solution().largestNumber([3, 30, 34, 5, 9]) )  # 输出: "9534330"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

['3', '30', '34', '5', '9'] 推演

# 初始值 ['3', '30', '34', '5', '9']
330 > 303     =>  ['3', '30', '34', '5', '9']    #不变
3034 < 3430   =>  ['3', '34', '30', '5', '9']    #交换
305 < 530     =>  ['3', '34', '5', '30', '9']    #交换
309 < 930     =>  ['3', '34', '5', '9', '30']    #交换
# 第二次循环 ['3', '34', '5', '9',    '30']   30已经放到最后了，只需要比较前面4个数据

1
2
3
4
5
6

# 16.分发糖果

135.分发糖果 (opens new window)
n 个孩子站成一排给你一个整数数组 ratings 表示每个孩子的评分
你需要按照以下要求，给这些孩子分发糖果：
- 每个孩子至少分配到 1 个糖果
- 相邻两个孩子评分更高的孩子会获得更多的糖果
请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果

1
2
3

1、Python

初始化糖果数组，每个孩子至少得到1颗糖果
从左到右遍历，确保右侧评分更高的孩子得到更多糖果
然后从右到左遍历，确保左侧评分更高的孩子得到更多糖果

class Solution:
    def candy(self, ratings):
        n = len(ratings)
        candies = [1] * n      # 初始化糖果数组，每个孩子至少得到1颗糖果
        for i in range(1, n):  # 从左到右遍历，确保右侧评分更高的孩子得到更多糖果
            if ratings[i] > ratings[i - 1]:
                # 如果当前孩子的评分高于前一个孩子，糖果数应比前一个孩子多1
                candies[i] = candies[i - 1] + 1

        for i in range(n - 2, -1, -1):   # 从右到左遍历，确保左侧评分更高的孩子得到更多糖果
            if ratings[i] > ratings[i + 1]:
                # 如果当前孩子的评分高于后一个孩子，糖果数应比后一个孩子多1
                candies[i] = max(candies[i], candies[i + 1] + 1)
        return sum(candies)

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 17.每日温度

739.每日温度 (opens new window)
给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer
其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后
如果气温在这之后都不会升高，请在该位置用 0 来代替

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

1
2

1、Python

使用栈用于存储未找到更高温度的下标（栈顶温度是栈中最小的）
当前温度高于栈顶温度, 计算天数的差更新到 res数组对应位置
将当前天的下标入栈 (栈为空或当前温度小于等于栈顶温度)

class Solution:
    def dailyTemperatures(self, temperatures):
        nums = temperatures
        res = [0] * len(nums) # 初始值为 0，表示如果没有找到更高的温度则保持为0
        stack = []            # 栈用于存储未找到更高温度的下标（栈顶温度是栈中最小的）
        
        for i in range(len(nums)):
            # 当前温度高于栈顶温度, 计算天数的差更新到 res数组对应位置
            while stack and nums[i] > nums[stack[-1]]:
                top_index = stack.pop()         # 获取栈顶下标
                res[top_index] = i - top_index  # 计算天数差并存入结果数组
            stack.append(i)  # 将当前天的下标入栈 (栈为空 或 当前温度小于等于栈顶温度)

        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 18.跳跃游戏

55.跳跃游戏 (opens new window)
给你一个非负整数数组 nums ，你最初位于数组的第一个下标数组中的每个元素代表你在该位置可以跳跃的最大长度(可以比当前长度小)
判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false

输入：nums = [2,3,1,1,4]   输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标

输入：nums = [3,2,1,0,4]   输出：false
解释：无论怎样，总会到达下标为 3 的位置，但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标

1
2
3
4
5

1、Python

变量 max_ 用于记录当前能够到达的最远位置
i > max_成立，证明无法到达当前 i位置直接返回 False
否则更新max_为当前可到达的最远位置（当前i位置坐标+当前能跳的最大位置）
如果max_已经能够到达或超过最后一个下标，返回True

class Solution:
    def canJump(self, nums):
        max_ = 0         # 变量 max_ 用于记录当前能够到达的最远位置
        for i in range(len(nums)):
            if i > max_:   # i 超出了 max_ 无法达到当前 i 位置，直接返回 False
                return False
            else:
                # 更新max_为当前可到达的最远位置（当前i位置坐标+当前能跳的最大位置）
                max_ = max(max_, i + nums[i])
                # 如果max_已经能够到达或超过最后一个下标，返回True
                if max_ >= len(nums) - 1:
                    return True
        return False # 如果遍历结束后，max_ 仍未到达最后一个下标，返回False

print( Solution().canJump([3,2,1,0,4]) )    # False
""" [3,2,1,0,4] 输出 False 推演 max(max_, i + nums[i]) 
i=0  max_=max(0, 0+3)=3
1=1  max_=max(3, 1+2)=3
i=2  max_=max(3, 2+1)=3
i=3  max_=max(3, 3+0)=3
i=4  max_=3 不符合 i <= max_ 所以最终返回 False
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 19.跳跃游戏 II

45.跳跃游戏 II (opens new window)
给定一个长度为 n 的整数数组 nums初始位置为 nums[0]
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处
返回到达 nums[n - 1] 的最小跳跃次数

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2，从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置

1
2
3

1、Python

对于每个位置，计算可以达到的最远位置 tmp_max
如果当前位置是当前跳跃的最远位置 max_，则更新 max_ 为 tmp_max，并增加跳跃次数 steps
如果当前位置 i 等于 max_，我们需要进行一次跳跃，以便扩展跳跃范围，继续前进（否则未到达最远位置不增加跳跃次数）

class Solution:
    def jump(self, nums):
        steps = 0            # 跳跃次数
        max_ = 0             # 当前跳跃能到达的最远位置
        tmp_max = 0          # 遍历过程中能到达的最远位置

        for i in range(len(nums) - 1):
            # 更新当前跳跃范围内能到达的最远位置
            # `nums[i] + i` 表示从当前位置 `i` 能跳到的最远位置
            tmp_max = max(nums[i] + i, tmp_max)
            # 当前位置 i 等于 max_，我们需要进行一次跳跃，以便扩展跳跃范围，继续前进
            if i == max_:
                max_ = tmp_max             # 更新当前跳跃范围的结束位置
                steps += 1
                if max_ >= len(nums) - 1:  # 如果可以到达最后一个位置，提前结束
                    break
        return steps

print( Solution().jump([3,2,1,3,2,1]) )    # 输出 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 20.字母异位词分组

49.字母异位词分组 (opens new window)
给你一个字符串数组，请你将 字母异位词 组合在一起可以按任意顺序返回结果列表
字母异位词 是由重新排列源单词的所有字母得到的一个新单词

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

输入: strs = [""]
输出: [[""]]

1
2
3
4
5

1、Python

使用一个字典来存储字母异位词组，字典key使用字母异位词组排序
只要是字母异位词组，排序后结果肯定是一样的，存储即可
{'aet': ['eat', 'eat', 'tea'], 'ant': ['nat']}

class Solution:
    def groupdic(self, strs):
        dic = {}                       # 初始化一个空字典，用于存储字母异位词组
        for s in strs:
            key = ''.join(sorted(s))   # 将字符串排序，得到字母异位词的唯一标识
            if key not in dic:         # 如果key不在字典中，则创建一个新的列表
                dic[key] = []
            dic[key].append(s)         # 将原字符串加入对应的字母异位词组中
        return list(dic.values())      # 返回所有字母异位词组

print( Solution().groupdic(["eat", "eat", "tea", "nat"]) )  # [['eat', 'eat', 'tea'], ['nat']]

1
2
3
4
5
6
7
8
9
10
11

# 21.加油站

134.加油站 (opens new window)
在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升
你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升
你从其中的一个加油站出发，开始时油箱为空
给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1
如果存在解，则 保证 它是 唯一 的

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油，此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站
因此，3 可为起始索引

1
2
3
4
5
6
7
8
9
10

1、Python

只要所有的总油量大于等于总消耗就可以保证可以返回（因为起点可以自己选择）
当油量不足以支持前进时，需要将起点移到下一个加油站，继续尝试
题目中已说明如果存在解，则解是唯一的，这意味着我们只需找到那个起始点即可

class Solution:
    def canCompleteCircuit(self, gas, cost):
        record = 0          # 总油量-总消耗（减去）
        cur = 0             # 当前油量-当前消耗（减去）
        start_index = 0     # 起始站点索引

        for i in range(len(gas)):
            record += gas[i] - cost[i] # gas[i]（加油站汽油量）- cost[i]（下一个加油站消耗量）
            cur += gas[i] - cost[i]    # 更新当前油量与当前消耗的差值
            if cur < 0:                # 如果当前油量不足以前进到下一个站点
                start_index = i + 1    # 将起点设置为下一个站点
                cur = 0                # 重置当前油量，因为我们从新的站点重新开始

        return start_index if record >= 0 else -1  # 总油量大于等于总消耗，返回起始站点索引，否则返回 -1

print( Solution().canCompleteCircuit([1,2,3,4,5], [3,4,5,1,2]) )

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

上次更新: 2025/3/25 17:29:52

← 06.动态规划 04.数组_双指针_排序_子数组→

01.数组

# ① 数组操作

# 01.买卖股票的最佳时机

# 02.买卖股票的最佳时机II

# 03.删除有序数组中重复项

# 04.2 删除有序数组中的重复项 II

# 05.找到所有数组中消失的数字

# 06.缺失的第一个正数

# 07.移动零

# 08.两个数组的交集

# 09.两个数组的交集 II

# 10.加一

# 11.列表连续相同数据放一起

# 12.下一个排列

#

# ② 其他

# 13.柱状图中最大的矩形

# 14.最长连续序列

# 15.最大数

# 16.分发糖果

# 17.每日温度

# 18.跳跃游戏

# 19.跳跃游戏 II

# 20.字母异位词分组

# 21.加油站

# `① 数组操作`