不做大哥好多年
xiaonaiqiang
2021-04-06
目录

03.递归

# 01.递归

# 1.1 递归讲解

  • 1、定义

    • 在函数内部，可以调用其他函数
    • 如果一个函数在内部调用自身本身，这个函数就是递归函数

  • 2、递归特性

    • 1.必须有一个明确的结束条件

    • 2.每次进入更深一层递归时，问题规模相比上次递归都应有所减少

    • 3.递归效率不高，递归层次过多会导致栈溢出（在计算机中，函数调用是通过栈（stack）这种数据结构实现的

    • 4.每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧

    • 5.由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出）

def dfs(n):
    if n > 3:
        return n
    dfs(n+1)
    print(n)
    return n
print("res", dfs(1))
"""
3
2
1
res 1
"""
1
2
3
4
5
6
7
8
9
10
11
12
13

# 1.2 递归原理讲解

  • 1.每一次函数调用都会有一次返回，并且是某一级递归返回到调用它的那一级，而不是直接返回到main()函数中的初始调用部分

  • 2.第一次递归：n=3入栈【3】

  • 3.第二次递归：n=2入栈【3,2】

  • 4.第三次递归：n=1入栈【3,2,1】

  • 5.当n=0时0>0为False，不再递归，print num=0,函数返回到调用他的上一级，即栈顶n=1

  • 6.接着位置digui(num-1)向下执行：此时打印printnum=1,1出栈，栈中元素：【3,2】

  • 7.依次类推会打印2,3所以最终打印结果如右图

  • 8.图解

#! /usr/bin/env python
# -*- coding: utf-8 -*-
def digui(num):
    print num
    if num > 0:
        digui(num - 1)
    else:
        print '------------'
    print num

digui(3)

''' 执行结果
3
2
1
0
------------
0
1
2
3
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 1.3 结果剖析

  • 1.为什么会得出上面的结果呢？因为都把调用函数本身之后的代码给忘记了，就是else之后的python 代码

  • 2.在调用函数本身时，它之后的代码并没有结束，而是在等待条件为False 时，再接着执行之后的代码，同一个颜色的print()语句等待对应颜色的函数

  • 3.下面我把此递归函数做了一个分解，详解递归函数，当调用递归函数digui(3)时，执行过程如下：

# 02.求阶乘代码

# 2.1 代码

#! /usr/bin/env python
# -*- coding: utf-8 -*-
def test(n):
    if n == 1:
        return 1
    else:
        res = n*test(n-1)
        print( "n:%s-----ret:%s"%(n, res) )
    return res

print( test(4) )  # 24
'''
n:2-----ret:2
n:3-----ret:6
n:4-----ret:24
24
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 2.2 求4的阶乘递归推演

# 1、递归步骤
'''
1、第一层：test(4) = 4*test(4-1)
2、第二层：test(3) = 3*test(3-1)
3、第三层：test(2) = 2*test(2-1)
4、第四层：test(1) = 1
'''

# 2、返回步骤
'''
注：上层调用的位置都是：res = n*test(n-1)，所以返回上层后会接着这里向下执行知道return
5、n=1那么就会执行if代码块内的代码return 1此时第四层函数结束： ret = 1
6、第四层函数结束后会接着第三层调用的位置向下执行直到return：  ret = 1 * 2
7、第三层函数返回后会回到第二层调用位置return：                ret = 1 * 2 * 3
8、第二层函数返回后会回到第一层调用位置return:                 ret = 1 * 2 * 3 * 4
到达第一层调用位置后，没有上层的递归调用位置，此时函数才会正真返回
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
  • 步骤图解

# 03.求树的高度

# 3.1 代码

class TreeNode:
	def __init__(self, val=0, left=None, right=None):
		self.val = val
		self.left = left
		self.right = right

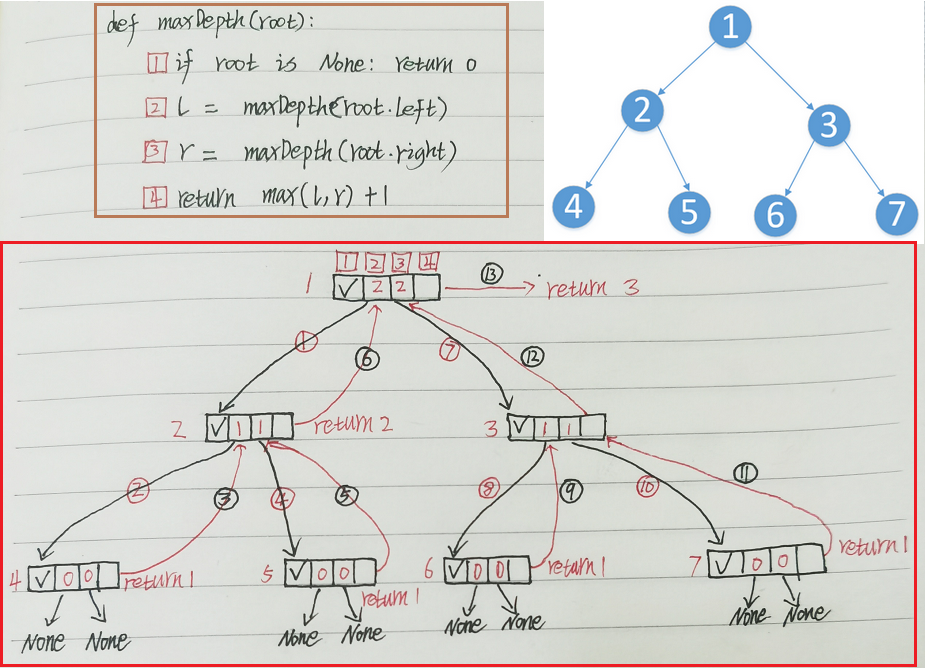
def maxDepth(root):
	if root is None: return 0
	l = maxDepth(root.left)
	r = maxDepth(root.right)
	return max(l, r) + 1

if __name__ == '__main__':
	root = TreeNode(3,
					left=TreeNode(9),
					right=TreeNode(20, TreeNode(15), TreeNode(7, TreeNode(10)))
					)
	print(maxDepth(root))  # 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 3.2 步骤解释

# 步骤 1：从根节点 1 开始
1
#  步骤 1：maxDepth(1) 
执行 l = maxDepth(root.left) => maxDepth(2)
#  步骤 2：maxDepth(2)
执行 l = maxDepth(root.left) => maxDepth(4)
#  步骤 3：maxDepth(4)
执行 l=maxDepth(root.left)   => maxDepth(None) return 0
执行 r=maxDepth(root.right)  => maxDepth(None) return 0
maxDepth(4)=return max(l, r) + 1  => max(0, 0) + 1  return 1 （4返回1）

# 回溯到节点2
l=maxDepth(root.left) => maxDepth(4) = 1
接着执行 r=maxDepth(root.right) => maxDepth(5)

#  步骤 4：maxDepth(5)
执行 l=maxDepth(root.left)   => maxDepth(None) return 0
执行 r=maxDepth(root.right)  => maxDepth(None) return 0
maxDepth(5)=return max(l, r) + 1    => max(0, 0) + 1  return 1 （5返回1）

# 回溯到节点2
l=maxDepth(root.left)   => maxDepth(4) return 1 （来做上面4返回）
r=maxDepth(root.right)  => maxDepth(5) return 1 （来做上面5返回）
接着执行
maxDepth(2)=return max(l, r) + 1    => max(1, 1) + 1  return 2 （2返回2）

# 回溯到节点1
l=maxDepth(root.left) => maxDepth(2) = 2 （来做上面4返回）
接着执行 r=maxDepth(root.right) => maxDepth(3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 04.深度优先全排列

  • 全排列 (opens new window)

  • 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 你可以 按任意顺序 返回答案

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]
1
2
3
4
5
6
7
8
  • 时间复杂度为 O(n * n!)
    • 生成一个排列需要遍历列表中的每个元素，并且有 n!（1*2*3*n!） 种不同的排列
    • 对于每一个排列，生成的过程涉及递归深度为 n，并且每层递归都需要遍历所有 n 个元素
  • 空间复杂度为 O(n) 加上结果存储的空间 O(n * n!)
    • 递归栈空间: 由于递归调用的深度为 n，因此递归栈空间的复杂度为 O(n)
    • 附加存储空间: 需要一个数组来跟踪哪些元素已经被使用 (used 数组)，以及保存当前排列 (path 数组)，这些也都是 O(n) 的空间
    • 结果存储空间: 生成的所有排列需要存储，占用 O(n * n!) 的空间

# 1、python回溯算法

  • 对于一个给定的数组，DFS会从头到尾依次选择一个元素作为排列的一部分

  • 然后对剩余元素继续递归，直到生成一个完整的排列当所有排列都生成后，递归结束

  • 递归函数 dfs:
    • path 保存当前排列路径
    • used 是一个布尔数组，标记哪些元素已经被使用过
    • res 是存放所有排列结果的列表
  • 递归逻辑:
    • 在递归函数中，我们遍历 nums 的每一个元素，通过检查 used[i] 是否为 False，判断该元素是否已经被使用过
    • 如果未被使用，则将其加入 path 并标记为已使用，继续递归处理剩下的元素
    • 在递归返回后，通过 pop() 和 used[i] = False 撤销选择，进行回溯

class Solution:
    # path（排列路径）user（哪些使用过） res(排列结果列表)
    def permute(self, nums):
        def dfs(path, used, res):
            if len(path) == len(nums):  # 找到一个完整的排列
                res.append(path[:])  # path[:] 创建了一个浅拷贝
                return

            # 遍历每个数字，尝试将其加入当前排列路径中
            for i in range(len(nums)):
                if used[i]:  # 如果当前数字被使用过 跳过
                    continue

                path.append(nums[i])  # 选择当前数字
                used[i] = True

                dfs(path, used, res)  # 递归处理剩余的数字

                path.pop()  # 回溯：撤销选择
                used[i] = False

        res = []
        used = [False] * len(nums)
        dfs([], used, res)
        return res

# 示例输入
nums = [1, 2, 3]
print(Solution().permute(nums))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 2、回溯执行梳理

  • 在递归调用中，每一层递归都会有自己的 for i in range(len(nums)) 循环

  • 当程序回溯到上一层时，它会继续执行该层的 for 循环，而不是从头重新开始这个循环

  • 就是说，回溯（即 pop 操作后），程序会回到上一层的递归继续执行，并不会重置 i 的值

# 0、说明

  • 左子树回溯时 i 的值在递增，直到所有 i 被处理完，因为回溯时 for 循环继续从 i 的下一个值开始

    • 因为左子树在回溯的过程中，used 状态会被重置为 False
    • 所以当继续遍历时，不会因为 used[i] 已经被设置为 True 而跳过某些 i
    • 因此 for 循环会继续递增处理接下来的 i 值
    • 这就是为什么左子树回溯时，i 会继续递增直到所有可能的 i 都被处理完

  • 右子树回溯时会先处理当前 i 的状态，然后再继续回溯，是因为该层递归中的 i 还未遍历完，因此要继续当前 for 循环

    • 在右子树中，有些 i 的值已经被设置为 True，并且在当前递归层还没有回溯完成
    • 所以在 for 循环中，当 if not used[i] 条件被检查时，可能会直接跳过已经被使用的 i
    • 从而导致当前 i 的循环无法继续
    • 这就是为什么在右子树的情况下，递归层需要处理当前 i 的状态后，再继续回溯或结束递归

# 1、执行i=0左子树递归

第一层递归 (i=0, 选择 1):

  • path = [1]，used = [True, False, False]
  • i = 0执行 path.append(nums[1]) 生成path = [1]，used = [True, False, False]

第二层递归 (i=1, 选择 2):

  • path = [1, 2]，used = [True, True, False]
  • 第二层是一个全新的开始 从 i=0开始执行
  • i = 0 used[0] = True 跳过
  • i = 1执行path.append(nums[1]) 生成path = [1, 2]，used = [True, True, False]

第三层递归 (i=2, 选择 3):

  • path = [1, 2, 3]，used = [True, True, True]
  • 第三层是一个全新的开始 从 i=0开始执行
  • i = 0 used[0] = True 跳过
  • i = 1 used[1] = True 跳过
  • i = 2 执行path.append(nums[2]) 生成path = [1, 2, 3]，used = [True, True, True]
  • len(path) == len(nums) 为True，res添加 [1, 2, 3]
  • 第三层for循环全部结束，向第二层回溯

回溯到第二层 (i=2, 回溯):

  • path = [1, 2]，used = [True, True, False]

  • 第二层i=0, i=1 都已经执行过，回溯到第二层从 i=2执行（左子树从 i 的下一个值开始）

  • 执行path.pop()，used[2] = False 回到 path = [1, 2]，used = [True, True, False]

  • 回到第二层的 for 循环，这里的 i=2 已经完成处理，所以该层递归结束，继续回溯到第一层

回溯到第一层 (i=1, 回溯):

  • path = [1]，used = [True, False, False]

  • 第一层i=0 已经执行过，回溯到第一层从 i=1执行（左子树从 i 的下一个值开始）

  • i=1执行path.pop()，used[1] = False 回到 path = [1]，used = [True, False, False]

  • 到目前位置第一层只执行到 i=1 需要继续执行i=2

# 2、执行i=0右子树递归

第一层递归 (i=2, 选择3):

为什么从 i=2 开始

  • 在递归调用中，i 的值是在每一层递归的 for 循环中独立管理的
  • 当你回溯到第一层递归时，i 的值会继续从上一层未完成的位置开始，即 i=2
  • 这是因为 i 的值是在 for 循环中持久化的，回溯只是撤销了之前的选择，并不会重置 i 的值
  • path = [1, 3]，used = [True, False, True]
  • i=2 执行path.append(nums[2]) 生成path = [1, 3]，used = [True, False, True]
  • 此时 第一层for循环全部结束，执行第二层

第二层递归 (i=1, 选择 2)

  • 在这个新的第二层递归中，for i in range(len(nums)) 循环从 i=0 开始

  • 会创建一个新的栈帧，在这个新的栈帧中，for 循环从 i=0 开始独立执行，与之前的状态无关

  • 因此，这个新的第二层递归会重新检查所有的 i 值

  • 在这个新的第二层递归中，for i in range(len(nums)) 循环从 i=0 开始
  • i = 0 used[0] = True 跳过
  • i = 1 执行path.append(nums[1]) 生成path = [1, 3, 2]，used = [True, True, True]

第三层递归 (i=1, 选择 2)

  • 此时 len(path) == len(nums)，将 [1, 3, 2] 加入结果集 res = [[1, 2, 3], [1, 3, 2]]
  • 第三层因为满足 len(path) == len(nums) 条件，直接返回了

回溯到第二层 (i=2, 回溯):

  • path = [1, 3]，used = [True, False, True]

  • 从第三层回溯到第二层，当前状态i = 1 （右子树继续当前 for 循环）

  • i=1执行path.pop()，used[1] = False 回到 path = [1, 3]，used = [True, False, True]

  • i=2 used[0] = True 跳过

  • 由于这一层的 for 循环中的所有 i 值都已经处理过，这层递归结束，回溯到第一层递归

回溯到第一层 (i=1, 回溯):

  • path = [1]，used = [True, False, False]

  • 从第二层回溯到第一层，当前状态i=2 （右子树继续当前 for 循环）

  • i=2执行path.pop()，used[2] = False 回到 path = [1]，used = [True, False, False]

回到初始状态第0层

  • path = []，used = [False, False, False]

  • 从第一层回溯到第0层，当前状态i = 0 （右子树继续当前 for 循环）

  • i=0执行path.pop()，used[0] = False 回到 path = []，used = [False, False, False]

  • 此时只是完成了第0层 i=0 第递归遍历，下面在第0层开始 i=1的递归遍历

# 3、执行i=1左子树递归

第一层递归 (i=1, 选择 2):

  • path = [2]，used = [False, True, False]
  • i=1 执行 path.append(nums[1]) 生成path = [2]，used = [False, True, False]

第二层递归 (i=1, 选择 2):

  • path = [2, 1]，used = [True, True, False]
  • 第二层是一个全新的开始 从 i=0开始执行
  • i = 0执行path.append(nums[1]) 生成path = [2, 1]，used = [True, True, False]

第三层递归 (i=2, 选择 3):

  • 第三层是一个全新的开始 从 i=0开始执行
  • i = 0，i = 1都是True，直接跳过
  • i = 2执行 path.append(nums[2]) 生成path = [2, 1, 3]，used = [True, True, True]
  • 找到完整排列，保存结果并回溯
上次更新: 2024/9/11 16:38:01
02.遍历树
04.算法模型

← 04.算法模型→

最近更新
01
16.CAP
09-27
02
13.HTTP协议
09-25
03
12.TCP协议
09-25
更多文章>
Theme by Vdoing | Copyright © 2019-2024 逍遥子 技术博客 京ICP备2021005373号