不做大哥好多年
xiaonaiqiang
2021-03-14
目录

02.遍历树

# 01.树的遍历

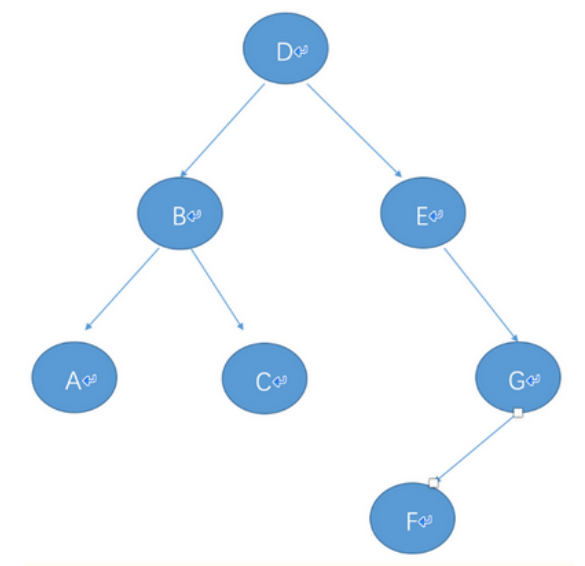
# 1.1 生成树结构

  • 1.前序遍历： DBACEGF（根节点排最先，然后同级先左后右）
  • 2.中序遍历： ABCDEFG (先左后根最后右）
  • 3.后序遍历： ACBFGED （先左后右最后根）

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
1
2
3
4
5
6
7
8
9
10

# 1.2 先根遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def preTraverse(root):
     '''
     前序遍历
     '''
     if root==None:
         return
     print(root.value)
     preTraverse(root.left)
     preTraverse(root.right)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('前序遍历：')
    preTraverse(root)   #  DBACEGF
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 先根遍历步骤推演

函数调用中的栈帧

  • 每当函数被调用时，系统会为这个函数调用创建一个栈帧（Stack Frame）

  • 当函数执行完毕后，它的栈帧会被移除，控制权回到上一个函数调用的位置

  • 在递归过程中，函数会不断调用自己，每一次调用都会创建一个新的栈帧，并将其压入到调用栈中

  • 当递归达到基线条件（比如节点为 None）时，递归开始返回，栈帧逐个弹出

  • 前序遍历： DBACEGF（根节点排最先，然后同级先左后右）

1）访问根节点：

  • 从树的根节点开始，将当前节点 root = Node(D) 作为当前节点并输出其值 D，此时 D 入栈，栈状态为 [D]

2）访问左子树：

  • 递归调用 preTraverse(root.left)，将当前节点移到 Node(D) 的左子节点 Node(B)
  • 输出其值 B，并将 B 入栈，栈状态为 [D, B]

3）继续访问左子树的左子树：

  • 递归调用 preTraverse(root.left)，将当前节点移到 Node(B) 的左子节点 Node(A)
  • 输出其值 A，并将 A 入栈，栈状态为 [D, B, A]

4）左子树遍历结束：

  • 当前节点 Node(A) 的左子节点为 None，此时返回上层调用，顺序执行 preTraverse(root.right)
  • 当前节点 Node(A) 的右子节点也是 None，整个子树遍历完毕
  • 函数返回，A 出栈，栈状态为 [D, B]

5）访问左子树的右子树：

  • 返回到 Node(B)，执行 preTraverse(B.right)，将当前节点移到 Node(B) 的右子节点 Node(C)
  • 输出其值 C，并将 C 入栈，栈状态为 [D, C]

6）左右子树遍历结束：

  • 当前节点 Node(C) 的左子节点和右子节点都为 None，遍历完毕，函数返回
  • C 出栈，返回上层调用，栈状态为 [D]

7）左子树遍历结束：

  • 返回到 Node(D)，执行 preTraverse(D.right)，将当前节点移到 Node(D) 的右子节点 Node(E)
  • 输出其值 E，并将 E 入栈，栈状态为 [E]

8）继续访问右子树：

  • 递归调用 preTraverse(root.left)，发现 Node(E) 的左子节点为 None，直接返回
  • 接着执行 preTraverse(root.right)，移动到 Node(E) 的右子节点 Node(G)
  • 输出其值 G，并将 G 入栈，栈状态为 [E, G]

9）访问右子树的左子树：

  • 当前节点 Node(G) 的左子节点 Node(F) 被访问，输出其值 F，并将 F 入栈，栈状态为 [E, G, F]

10）右子树遍历结束：

  • 当前节点 Node(F) 的左右子节点均为 None，遍历完毕，函数返回，F 出栈
  • 栈状态为 [E, G]，接着 G 出栈，栈状态为 [E]，最后 E 出栈，栈状态为空，前序遍历完成

# 1.3 中根遍历

  • ABCDEFG (先左后根最后右）

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def midTraverse(root):
    '''
    中序遍历
    '''
    if root == None:
        return
    midTraverse(root.left)
    print(root.value)
    midTraverse(root.right)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('中序遍历：')
    midTraverse(root)   #  ABCDEFG  (先左后根最后右）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 1.4 后根遍历

  • 后序遍历： ACBFGED （先左后右最后根）

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def afterTraverse(root):
    '''
    后序遍历
    '''
    if root == None:
        return
    afterTraverse(root.left)
    afterTraverse(root.right)
    print(root.value)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('后序遍历：')
    afterTraverse(root)   #  ACBFGED
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 1.5 分层打印二叉树

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self, value=None, left=None, right=None):
        self.value = value
        self.left = left  # 左子树
        self.right = right  # 右子树

def layer(root):
    curLayer = [root]  # 当前层的节点
    while curLayer:    # 只要当前层有节点就循环
        layerValue = []   # 当前层节点对应的值
        nextLayer = []    # 下一层节点
        for node in curLayer:  # 循环当前节点
            layerValue.append(node.value)  # 添加当前层节点的值
            if node.left:
                nextLayer.append(node.left)  # 添加下一层节点左节点
            if node.right:
                nextLayer.append(node.right)  # 添加下一层节点右节点
        print(layerValue)  # 打印当前层的值
        curLayer = nextLayer  # 移动到下一层


if __name__ == '__main__':
    root = Node('D', Node('B', Node('A'), Node('C')), Node('E', right=Node('G', Node('F'))))
    layer(root)

'''
['D']
['B', 'E']
['A', 'C', 'G']
['F']
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 02.广度优先

  • D B E A C G F

# 2.1 栈实现BFS

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self, value=None, left=None, right=None):
        self.value = value
        self.left = left  # 左子树
        self.right = right  # 右子树

# 广度优先搜索
def bfs(root):
    res = []
    q = [root] # 先把根节点放进队列中
    while q:  # 当队列不为空时进入循环体
        current_node = q.pop(0)  # 取出队列的第一个节点
        print(current_node.value)
        if current_node.left:   # 如果左子树不为空，就加入队列
            q.append(current_node.left)
        if current_node.right:  # 如果右子树不为空，就加入队列
            q.append(current_node.right)
    return res

if __name__ == '__main__':
    root = Node('D', Node('B', Node('A'), Node('C')), Node('E', right=Node('G', Node('F'))))
    bfs(root)  # D B E A C G F
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 2.2 分层思想

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self, value=None, left=None, right=None):
        self.value = value
        self.left = left  # 左子树
        self.right = right  # 右子树

def bfs(root):
    curLayer = [root]  # 当前层的节点
    while curLayer:    # 只要当前层有节点就循环
        nextLayer = []    # 下一层节点
        for node in curLayer:  # 循环当前节点
            print(node.value)
            if node.left:
                nextLayer.append(node.left)  # 添加下一层节点左节点
            if node.right:
                nextLayer.append(node.right)  # 添加下一层节点右节点
        curLayer = nextLayer  # 移动到下一层

if __name__ == '__main__':
    root = Node('D', Node('B', Node('A'), Node('C')), Node('E', right=Node('G', Node('F'))))
    bfs(root)  # D B E A C G F
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 03.深度优先

  • D B A C E G F

# 3.1 栈实现DFS

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self, value=None, left=None, right=None):
        self.value = value
        self.left = left  # 左子树
        self.right = right  # 右子树

# 深度优先搜索
def dfs(root):
    res = []
    q = [root]   # 先把根节点放进栈中
    while q:     # 当栈不为空时进入循环体
        current_node = q.pop()  # 取出栈顶节点
        print(current_node.value)
        if current_node.right:  # 如果右子树不为空，就压入栈
            q.append(current_node.right)
        if current_node.left:  # 如果左子树不为空，就压入栈
            q.append(current_node.left)
    return res

if __name__ == '__main__':
    root = Node('D', Node('B', Node('A'), Node('C')), Node('E', right=Node('G', Node('F'))))
    dfs(root)  # D B A C E G F
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 3.2 递归实现DFS

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self, value=None, left=None, right=None):
        self.value = value
        self.left = left  # 左子树
        self.right = right  # 右子树

# 深度优先搜索
# 使用递归实现深度优先搜索
def dfs_recur(node):
    if not node: # 递归结束的条件是当该节点为None时
        return
    print(node.value)
    dfs_recur(node.left) # 对左子树进行递归
    dfs_recur(node.right) # 对右子树进行递归

if __name__ == '__main__':
    root = Node('D', Node('B', Node('A'), Node('C')), Node('E', right=Node('G', Node('F'))))
    dfs_recur(root)  # D B A C E G F
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
上次更新: 2024/8/29 16:48:43
01.排序算法
03.递归

← 03.递归→

最近更新
01
16.CAP
09-27
02
13.HTTP协议
09-25
03
12.TCP协议
09-25
更多文章>
Theme by Vdoing | Copyright © 2019-2024 逍遥子 技术博客 京ICP备2021005373号