不做大哥好多年
xiaonaiqiang
2025-03-25
目录

06.回溯算法

# 回溯算法

# 601.子集

  • 场景：生成所有子集，不考虑顺序

  • 78.子集 (opens new window)

  • 给你一个整数数组 nums ，数组中的元素互不相同 返回该数组所有可能的子集

  • 解集不能包含重复的子集，你可以按 任意顺序 返回解集

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

输入：nums = [0]
输出：[[],[0]]
1
2
3
4
5

1、Python

  • 每次进入 backtrack 函数时，都会将当前的子集 path 加入到结果 result 中
  • 使用 for 循环从 start 开始遍历 nums，依次尝试将每个元素加入到当前子集中
  • 对于每个元素，先加入 path，然后递归调用 backtrack 以生成包括当前元素的子集
  • 递归完成后，使用 path.pop() 进行回溯，移除当前元素，继续生成不包括当前元素的子集
class Solution:
    def subsets(self, nums):
        res = []
        def dfs(start, path):
            res.append(path.copy())            # 每次进入函数时，都将当前路径（子集）添加到结果集中
            for i in range(start, len(nums)):  # 从start开始遍历，尝试构建不同的子集
                path.append(nums[i])           # 将当前元素加入到路径（子集）中
                dfs(i + 1, path)               # 递归调用dfs，继续构建包含当前元素的子集
                path.pop()                     # 回溯：移除当前元素，尝试构建不包含当前元素的子集
        dfs(0, [])                             # 初始调用时，路径为空，开始索引为0
        return res

print(Solution().subsets([1, 2, 3]))  # 输出：[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
1
2
3
4
5
6
7
8
9
10
11
12
13

时间复杂度: O(n \* 2^n)

  • 生成所有子集的复杂度: 每个元素可以选择在或不在某个子集中，因此有 2^n 个子集。

  • 构建每个子集的复杂度: 每次生成一个子集时，算法最多需要遍历 n 个元素。

空间复杂度：O(n * 2^n)

  • 最终结果 res 中包含 2^n 个子集，每个子集的最大长度为 n
  • 所以存储这些子集的空间复杂度为 O(n * 2^n)

# 602.和为目标不同组合

  • 39.组合总和 (opens new window)

  • 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target

  • 找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回

  • 你可以按 任意顺序 返回这些组合

  • candidates 中的 同一个 数字可以 无限制重复被选取

  • 如果至少一个数字的被选数量不同，则两种组合是不同的

  • 对于给定的输入，保证和为 target 的不同组合数少于 150 个

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

输入: candidates = [2], target = 1
输出: []
1
2
3
4
5
6
7
8

1、Python

  • 排序候选数组：虽然排序不是必须的，但排序有助于提前终止搜索，从而优化性能

  • 回溯函数：定义一个回溯函数 backtrack，该函数接收当前组合、剩余目标值和当前处理的候选数组起始索引

  • 递归探索：

    • 对于每个候选数字，首先检查是否可以继续加入当前组合（即剩余目标值减去当前数字不小于0）
    • 然后递归调用回溯函数以探索进一步的组合

  • 剪枝：

    • 如果当前剩余的目标值为0，表示找到一个有效组合，将其加入结果集中
    • 否则，如果目标值小于0，则终止当前路径的探索
class Solution:
    def combinationSum(self, candidates, target):
        nums = candidates
        def dfs(start, path, k):
            if k == 0:
                res.append(path.copy())
                return
            elif k < 0:            # 如果目标值小于0，终止搜索
                return

            for i in range(start, len(nums)):
                path.append(nums[i])
                dfs(i, path, k - nums[i])  # 因为数字可以重复使用，所以下一层递归仍从当前索引开始
                path.pop()

        nums.sort()
        res = []
        dfs(0, [], target)
        return res

print(Solution().combinationSum([2, 3, 5], 8))  # 输出 [[2, 2, 2, 2], [2, 3, 3], [3, 5]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 603.分割回文串

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]
1
2

1、Python

  • 将字符串切分结果展开成一棵树以后，可以发现结果集就是对这棵树进行dfs深度优先搜索的遍历结果
  • 对所有分割方案挨个进行回文判断，最后找到所有可能性
class Solution:
    def partition(self, s):
        ret = []  # ret 用于存储所有的分割方案
        def dfs(start, path):
            if start == len(s):
                ret.append(path.copy()) # 如果到达字符串末尾，说明找到一个有效分割方案，存储下来
                return

            for i in range(start, len(s)):
                if is_palindrome(s, start, i): # 检查子串 s[i:j+1] 是否为回文
                    path.append(s[start: i + 1])
                    dfs(i + 1, path)
                    path.pop()  # 回溯，撤销选择


        def is_palindrome(s, left, right):  # 检查子串 s[left:right+1] 是否为回文
            while left < right:
                if s[left] != s[right]:
                    return False
                left += 1
                right -= 1
            return True

        dfs(0, [])  # 从第 0 个位置开始进行回溯
        return ret

print(Solution().partition("aab"))  # 输出 [['a', 'a', 'b'], ['aa', 'b']]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

时间复杂度：近于 O(n * 2^n)， 其中 n 是字符串的长度

  • 每个字符都有可能成为一个单独的回文子串，或者是多个字符组合成的回文子串
  • 因此，可能的划分方式数量非常多，接近于划分问题的 2^n 次方复杂度
  • 判断回文的次数 时间复杂度是 O(n)

空间复杂度：O(n * 2^n)

  • 结果列表 ret 中存储了所有的有效分割方案
  • 如果所有字符都是回文子串，那么每个字符都可以形成一个单独的子串，这样的分割方案的数量为 2^(n-1)

# 604.全排列

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]
1
2
3
4
5
6
7
8

1、Python

  • 递归函数 dfs: path 保存当前排列路径, used 是一个布尔数组，标记哪些元素已经被使用过, res 是存放所有排列结果的列表
  • 在递归函数中，我们遍历 nums 的每一个元素，通过检查 used[i] 是否为 False，判断该元素是否已经被使用过
  • 如果未被使用，则将其加入 path 并标记为已使用，继续递归处理剩下的元素
  • 在递归返回后，通过 pop() 和 used[i] = False 撤销选择，进行回溯
  • 为什么全排列不需要传入start
    • 在子集问题中，start 参数的作用是避免重复选择已经考虑过的元素，从而防止生成重复的子集
    • 在排列问题中，每一个排列都是有序的，每个位置都需要尝试放入所有可能的元素
class Solution:
    # path（排列路径）user（哪些使用过） res(排列结果列表)
    def permute(self, nums):
        def dfs(path, used):
            if len(path) == len(nums):   # 找到一个完整的排列
                res.append(path.copy())  # path[:] 创建了一个浅拷贝
                return

            # 遍历每个数字，尝试将其加入当前排列路径中
            for i in range(len(nums)):
                if used[i]:  # 如果当前数字被使用过 跳过
                    continue

                path.append(nums[i])  # 选择当前数字
                used[i] = True

                dfs(path, used)  # 递归处理剩余的数字

                path.pop()  # 回溯：撤销选择
                used[i] = False

        res = []
        used = [False] * len(nums)
        dfs([], used)
        return res

nums = [1, 2, 3]
print(Solution().permute(nums))
# [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

""" # 如果没有used 判断结果会打印如下
[
    [1, 1, 1], [1, 1, 2], [1, 1, 3], 
    [1, 2, 1], [1, 2, 2], [1, 2, 3], 
    [1, 3, 1], [1, 3, 2], [1, 3, 3], 
    [2, 1, 1], [2, 1, 2], [2, 1, 3], 
    [2, 2, 1], [2, 2, 2], [2, 2, 3], 
    [2, 3, 1], [2, 3, 2], [2, 3, 3], 
    [3, 1, 1], [3, 1, 2], [3, 1, 3], 
    [3, 2, 1], [3, 2, 2], [3, 2, 3], 
    [3, 3, 1], [3, 3, 2], [3, 3, 3]
]
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

时间复杂度: O(n * n!)

  • 对于一个长度为 n 的数组 nums，其所有排列的数量是 n!（n 的阶乘）
  • 生成每个排列需要进行 n 层递归，每层递归要遍历 n 个元素，因此总体时间复杂度为 O(n * n!)

空间复杂度: O(n * n!)

  • 结果列表 res 中存储了 n! 个排列，每个排列的长度为 n，因此存储结果的空间复杂度为 O(n * n!)

# 605.生成括号

  • 特点：生成符合特定规则的结构或模式
  • 22.括号生成 (opens new window)
  • 数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合
  • 1 <= n <= 8
# 输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]
# 输入：n = 1
输出：["()"]
1
2
3
4

1、Python

  • 虽然 generate 函数没有显式的 for 循环，但是它通过两个条件判断递归地做出了两种选择，相当于隐式地进行了选择的遍历
  • 因此，递归的每一层都相当于一个 for 循环在遍历这两种可能性
class Solution:
    def generateParenthesis(self, n):
        res = []  # 存储所有有效的括号组合
        def dfs(s, l, r):
            if len(s) == n * 2:  # 长度达到 2n 时加入结果列表
                res.append(s)
                return
            if l < n:  # 如果左括号数量小于 n
                dfs(s + '(', l + 1, r)
            # 如果右括号数量大于左括号数量肯定不符合，不进入循环即可
            if r < l:
                dfs(s + ')', l, r + 1)

        dfs('', 0, 0)
        return res
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 606.复原IP地址

  • 93.复原IP地址 (opens new window)
  • 给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址
  • 这些地址可以通过在 s 中插入 '.' 来形成，你可以按任何顺序返回答案
输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

输入：s = "0000"
输出：["0.0.0.0"]
1
2
3
4
5

1、Python

  • 回溯法: 我们尝试在字符串的不同位置插入 .，并递归地检查剩余部分是否可以继续形成有效的 IP 地址

  • 有效性检查: 每一段 IP 地址都必须是有效的（即在 0 到 255 之间且没有前导零）

  • 终止条件: 当我们插入了 3 个 . 时，如果剩下的部分也是一个有效的 IP 段，那么我们可以构成一个完整的 IP 地址

class Solution:
    def restoreIpAddresses(self, s):
        def dfs(start, path):
            if len(path) == 4:
                # print(path)
                if start == len(s):            # 已经分成了4段, 且已经用完所有字符
                    ret.append(".".join(path)) # 将路径转换为IP地址并存储
                return                         # 结束递归，防止路径超过4段

            for i in range(start, min(start + 3, len(s))):  # 每段最多3个字符, len(s) 保证不越界
                seg = s[start: i + 1]
                # 检查段是否合法：小于等于255，且不能有前导零（除非是"0"）
                if (seg[0] == "0" and len(seg) > 1) or (int(seg) > 255):
                    continue
                path.append(seg)
                dfs(i + 1, path)   # 递归处理剩下的字符串
                path.pop()

        ret = []
        dfs(0, [])                 # 从第 0 个位置开始进行回溯
        return ret

print(Solution().restoreIpAddresses("25525511135"))  # 输出: ['255.255.11.135', '255.255.111.35']
# print(Solution().restoreIpAddresses("10111"))  # 输出: ['1.0.1.11', '1.0.11.1', '10.1.1.1']
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
  • 推演：打印所有path=4的可能
class Solution:
    def restoreIpAddresses(self, s):
        def dfs(start, path):
            if len(path) == 4:
                print(path)
            for i in range(start, min(start + 3, len(s))):  # 每段最多3个字符, len(s) 保证不越界
                seg = s[start: i + 1]
                path.append(seg)
                dfs(i + 1, path)  # 递归处理剩下的字符串
                path.pop()

        ret = []
        dfs(0, [])                # 从第 0 个位置开始进行回溯
        return ret

print(Solution().restoreIpAddresses("25525511135"))  # 输出: ['255.255.11.135', '255.255.111.35']

"""
['2', '5', '5', '2']
['2', '5', '5', '25']
['2', '5', '5', '255']
['2', '5', '52', '5']
['2', '5', '52', '55']
['2', '5', '52', '551']
['2', '5', '525', '5']
['2', '5', '525', '51']
['2', '5', '525', '511']
['2', '55', '2', '5']
['2', '55', '2', '55']
['2', '55', '2', '551']
省略...
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 607.电话号码的字母组合

  • 17.电话号码的字母组合 (opens new window)
  • 给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合，答案可以按 任意顺序 返回
  • 给出数字到字母的映射如下（与电话按键相同）注意 1 不对应任何字母

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

输入：digits = "2"
输出：["a","b","c"]
1
2
3
4
5

1、Python

class Solution:
    def letterCombinations(self, digits):
        if not digits:
            return []

        dic = {
            '2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
            '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'
        }

        def dfs(start, path):
            if start == len(digits):    # 如果索引到达数字字符串的末尾，表示组合已完成
                res.append(path)        # 将当前的字母组合添加到结果列表
                return

            chars = dic[digits[start]]   # 获取当前数字对应的字母
            for i in range(len(chars)):  # 遍历当前数字对应的所有字母
                char = chars[i]
                dfs(start + 1, path + char) # 递归生成下一个位置的字母组合

        res = []
        dfs(0, "")
        return res

print(Solution().letterCombinations("23"))       # ['ad', 'ae', 'af', 'bd', 'be', 'bf', 'cd', 'ce', 'cf']
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 608.组合总和 II

  • 40.组合总和 II (opens new window)
  • 给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合
  • candidates 中的每个数字在每个组合中只能使用一次
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
  [1,1,6],
  [1,2,5],
  [1,7],
  [2,6]
]
1
2
3
4
5
6
7
8

1、Python

  • 使用深度优先搜索（DFS）来构建组合。递归函数 dfs 用于探索所有可能的组合路径
  • 在每一次递归调用中，k 是通过减去当前选中的数字 nums[i] 来更新的（即 k - nums[i]）
class Solution:
    def combinationSum2(self, candidates, target):
        nums = candidates
        def dfs(start, path, k):
            if k == 0:
                res.append(list(path))
                return
            elif k < 0:      # 如果剩余目标值小于0，终止搜索
                return

            for i in range(start, len(nums)):
                if i > start and nums[i] == nums[i - 1]:  # 跳过重复元素，确保结果不重复
                    continue
                path.append(nums[i])
                dfs(i + 1, path, k - nums[i])  # 不允许重复使用数字，索引移动到下一个元素
                path.pop()

        nums.sort()  # 对数字进行排序，以便剪枝和去重
        res = []
        dfs( 0, [], target)
        return res

print(Solution().combinationSum2([10, 1, 2, 7, 6, 1, 5], 8))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 609.套餐内商品的排列顺序

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]
1
2
  • 排列方案的生成
    • 根据字符串排列的特点，考虑深度优先搜索所有排列方案
    • 即通过字符交换，先固定第 1 位字符（ n 种情况）
    • 再固定第 2 位字符（ n-1 种情况）
    • 最后固定第 n 位字符（ 1 种情况）

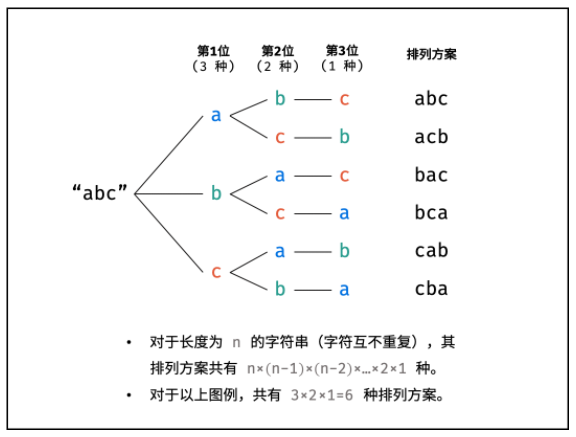
1、Python 回溯

class Solution:
    def goodsOrder(self, s):
        res = []
        s = sorted(s)                   # 先排序，方便去重
        def dfs(path, used):
            if len(path) == len(s):
                res.append("".join(path))
                return
            for i in range(len(s)):
                if used[i]:            # 如果该字符已被使用，跳过
                    continue
                # 如果多个字符相同，只处理最后一个，跳过重复元素
                if i > 0 and s[i] == s[i - 1] and not used[i - 1]:
                    continue
                used[i] = True
                dfs(path + [s[i]], used)
                used[i] = False

        dfs([], [False] * len(s))
        return res

print( Solution().goodsOrder("abc"))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
上次更新: 2025/4/29 17:38:19
04.数组_双指针_排序_子数组
08.动态规划

← 08.动态规划→

最近更新
01
04.数组双指针排序_子数组
03-25
02
08.动态规划
03-25
03
05.手写数字识别
03-13
更多文章>
Theme by Vdoing | Copyright © 2019-2025 逍遥子 技术博客 京ICP备2021005373号