01.树的概念

1、 二叉树

• 定义：每个节点最多有两个子节点，通常称为左子节点和右子节点
• 特点
  • 简单的树结构，适用于许多基本操作
  • 节点可以有零、一个或两个子节点
  • 常用于实现其他复杂树结构的基础，如二叉搜索树、堆等

2、二叉搜索树

• 定义：一种特殊的二叉树，每个节点的左子树的值小于该节点的值，右子树的值大于该节点的值
• 特点
  • 支持高效的插入、删除和查找操作，时间复杂度为O(log n)（对于平衡树）
  • 树的形状影响操作的效率，最坏情况下时间复杂度为O(n)

3、平衡二叉搜索树

• 定义：二叉搜索树的一种变体，通过维护树的平衡来保证操作的时间复杂度
• 特点
  • AVL树：保持每个节点的左右子树高度差不超过1
  • 红黑树：保持每个节点有额外的颜色属性，通过维护红黑性质来保持平衡
  • 时间复杂度：插入、删除和查找操作都为O(log n)

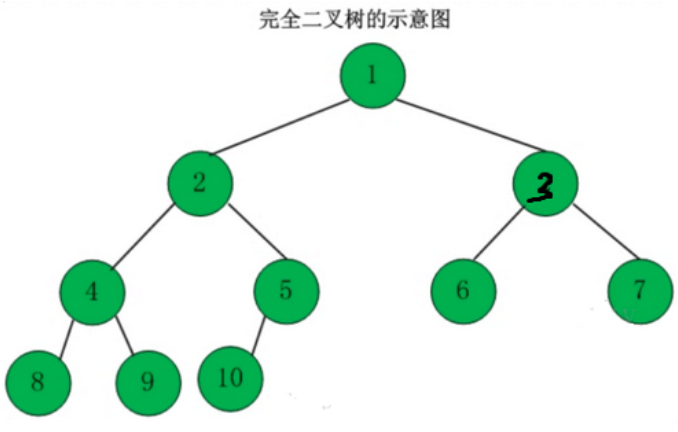
4、完全二叉树

• 1）若设二叉树的高度为h，除了第h层外，其他层的结点数都达到最大个数，第h层从右向左连续 缺若干个结点，则为完全二叉树

5、树的特点

• 1、如果一棵完全二叉树的父节点编号为K,则其左儿子的编号是2K,右儿子的结点编号为2K+1

• 2、已知完全二叉树的总节点数为n求叶子节点个数：

  • 当n为奇数时：（n+1）/2
  • 当n为偶数时 : （n）/2

• 3、已知完全二叉树的总节点数为n求父节点个数：为：n/2

• 4、已知完全二叉树的总节点数为n求叶子节点为2的父节点个数：

  • 当n为奇数时：n/2
  • 当n为偶数时 : n/2-1

• 5、如果一棵完全二叉树有N个结点，那么这棵二叉树的深度为【log2（N+1）log2（N+1）】（向上取整）

02.二叉树基本操作

2.1 数遍历说明

• 1. 前序遍历： DBACEGF（根节点排最先，然后同级先左后右）
• 2. 中序遍历： ABCDEFG (先左后根最后右）
• 3. 后序遍历： ACBFGED （先左后右最后根）

2.2 生成树结构

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))

2.3 前序遍历

2.3.1 前序遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def preTraverse(root):
     '''
     前序遍历
     '''
     if root==None:
         return
     print(root.value)
     preTraverse(root.left)
     preTraverse(root.right)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('前序遍历：')
    preTraverse(root)   #  DBACEGF

2.3.2 前序遍历步骤推演

前序排列原理：
#####此时执行preTraverse(root.left) 函数
'''
1、第一步 root=Node(D) print D，D入栈[D]
2、第二步 root=Node(D).left=Node(B) print B, B入栈[D,B]
3、第三步 root=Node(B).left=Node(A) print A, A入栈[D,B,A]
4、第四步 root=Node(A).left=None,没有进入递归，顺序执行preTraverse(root.right)
5、第五步 Node(A).right==None，也没有进入递归，此时preTraverse(A) 函数才会正真返回，A出栈[D,B]
6、第六步 A的上级调用函数为：preTraverse(B.left),所以接着会顺序执行preTraverse(B.right),B的左右节点访问后B出栈[D]
7、第七步 Node(B).right==Node(C) print C,C入栈[D,C]
8、第八步 Node(C).left==None, Node(C).right==None,访问完C的左右节点后函数返回C出栈，返回上级调用[D]
9、第九步 此时返回上级调用执行preTraverse(D.right)=Node(E) print E,D出栈，E入栈[E] 
'''

'''此时输出结果：DBACE'''

2.4 中序遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def midTraverse(root):
    '''
    中序遍历
    '''
    if root == None:
        return
    midTraverse(root.left)
    print(root.value)
    midTraverse(root.right)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('中序遍历：')
    midTraverse(root)   #  ACBFGED

2.5 后序遍历

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right   #右子树

def afterTraverse(root):
    '''
    后序遍历
    '''
    if root == None:
        return
    afterTraverse(root.left)
    afterTraverse(root.right)
    print(root.value)

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    print('后序遍历：')
    afterTraverse(root)   #  ACBFGED

2.6 分层打印二叉树

#! /usr/bin/env python
# -*- coding: utf-8 -*-
class Node:
    def __init__(self,value=None,left=None,right=None):
        self.value=value
        self.left=left    #左子树
        self.right=right  #右子树

def layered_print( root):
    if not root:
        return []
    curLayer = [root]                           # 当前层的所有节点
    while curLayer:
        layerValue = []                         # 当前层的值
        nextLayer = []                          # 下一层的所有节点
        for node in curLayer:                   # 循环当前层所有节点并并获取所有value值
            layerValue.append(node.value)
            if node.left:
                nextLayer.append(node.left)        # 将当前层的左节点加入列表
            if node.right:
                nextLayer.append(node.right)        # 将当前层的右节点加入列表
                
        print layerValue                           # 打印当前层的值
        curLayer = nextLayer                      # 将循环下移一层


'''
['D']
['B', 'E']
['A', 'C', 'G']
['F']
'''

if __name__=='__main__':
    root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
    layered_print(root)