不做大哥好多年
xiaonaiqiang
2025-03-25
目录

04.数组双指针排序_子数组

# ① 双指针/滑动窗口

# 101.两数之和

给定一个整数数组 nums 和一个整数目标值 target，
请你在该数组中找出 和为目标值 的那 两个 整数，并返回它们的数组下标
你可以假设每种输入只会对应一个答案但是，数组中同一个元素不能使用两遍
示例 1：
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1]
1
2
3
4
5
6
7

1、Python

class Solution:
    def twoSum(self, nums, target):
        dic = {}
        for k, v in enumerate(nums):
            if target - v in dic:  # 证明字典中存在一个value与当前value和等于target
                return [dic[target - v], k]
            dic[v] = k

Solution().twoSum([2, 11, 15, 3, 6, 7], 9)  # 3 4
1
2
3
4
5
6
7
8
9

2、Go

func twoSum(nums []int, target int) []int {
	tmpMap := map[int]int{}
	for index, num := range nums {
		if _, ok := tmpMap[target-num]; ok { // 证明字典中存在一个value与当前value和等于target
			return []int{tmpMap[target-num], index} // 返回这两个值的索引
		}
		tmpMap[num] = index
	}
	return []int{}
}
1
2
3
4
5
6
7
8
9
10

# 102.两数之和 II - 输入有序数组

输入：numbers = [2,3,4], target = 6
输出：[1,3]
输入：numbers = [-1,0], target = -1
输出：[1,2]
1
2
3
4

1、Python

  • 初始时两个指针分别指向第一个元素位置和最后一个元素的位置
  • 每次计算两个指针指向的两个元素之和，并和目标值比较
  • 如果两个元素之和等于目标值，则发现了唯一解
  • 如果两个元素之和小于目标值，则将左侧指针右移一位
  • 如果两个元素之和大于目标值，则将右侧指针左移一位
def twoSum(numbers, target):
    low, high = 0, len(numbers) - 1  # 初始时两个指针分别指向第一个元素位置和最后一个元素的位置
    while low < high:  # 只要左右指针没有相遇就循环
        total = numbers[low] + numbers[high]
        if total == target:   # 判断两个元素之和等于目标值，则发现了唯一解
            return [low + 1, high + 1]
        elif total < target:
            low += 1
        else:
            high -= 1
    return [-1, -1]

if __name__ == '__main__':
    numbers = [2,3,4]
    target = 6
    print( twoSum(numbers, target) )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 103.三数之和

  • 15.三数之和 (opens new window)

  • 给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？

  • 请你找出所有和为 0 且不重复的三元组

  • 注意：答案中不可以包含重复的三元组

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
1
2

1、Python

  • 对数组进行排序，遍历排序后数组
    • 若 nums[i]>0：因为已经排序好，所以后面不可能有三个数加和等于 0，直接返回结果
    • 对于重复元素：跳过，避免出现重复解
    • 令左指针 L=i+1，右指针 R=n-1，当 L<R 时，执行循环：
      • 当 nums[i]+nums[L]+nums[R]==0，执行循环
      • 判断左界和右界是否和下一位置重复，去除重复解
      • 并同时将 L,R移到下一位置，寻找新的解
        • 若和大于 0，说明 nums[R] 太大，R左移
        • 若和小于 0，说明 nums[L] 太小，L右移
class Solution:
    def threeSum(self, nums):
        n = len(nums)
        res = []
        if not nums or n < 3:  # 数组为 null 或者数组长度小于 3，返回 []
            return []
        nums.sort()  # 对数组进行排序
        if nums[0] > 0:  # 若 nums[0]>0：因为已经排序好，所以后面不可能有三个数加和等于 0，直接返回[]
            return []

        for i in range(0, n):  # 遍历排序后数组
            if i > 0 and nums[i] == nums[i - 1]:  # 对于重复元素：跳过，避免出现重复解
                continue

            L = i + 1
            R = n - 1
            while L < R:  # 令左指针 L=i+1，右指针 R=n-1，当 L<R 时，执行循环
                if nums[i] + nums[L] + nums[R] == 0:
                    res.append([nums[i], nums[L], nums[R]])
                    # 当 nums[i]+nums[L]+nums[R]==0，执行循环，判断左界和右界是否和下一位置重复，去除重复解
                    while L < R and nums[L] == nums[L + 1]:
                        L = L + 1
                    while L < R and nums[R] == nums[R - 1]:
                        R = R - 1
                    # 并同时将 L,R 移到下一位置，寻找新的解
                    L = L + 1
                    R = R - 1
                elif nums[i] + nums[L] + nums[R] > 0:  # 若和大于 0，说明 nums[R] 太大，R 左移
                    R = R - 1
                else:  # 若和小于 0，说明 nums[L] 太小，L 右移
                    L = L + 1
        return res


nums = [-1, 0, 1, 2, -1, -4]
print(Solution().threeSum(nums))  # [[-1, -1, 2], [-1, 0, 1]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# 104.盛最多水的容器

  • 11.盛最多水的容器 (opens new window)

  • 给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai)

  • 在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)

  • 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水

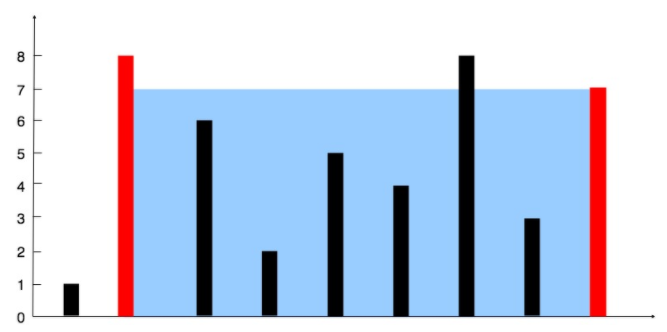
示例 1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49

示例 2：
输入：height = [1,1]
输出：1
1
2
3
4
5
6
7
8

1、Python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        l, r = 0, len(height) - 1
        max_water = 0

        while l < r:
            S = min(height[l], height[r]) * (r - l)        # 计算当前面积
            max_water = max(max_water, S)
            if height[l] < height[r]:        # 移动较矮的指针
                l += 1
            else:
                r -= 1

        return max_water
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 105.长度最小的子数组

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组
1
2
3

1、Python

  • 左右指针初始都指向0，列表开头位置
  • 右指针逐步向右移动，将新元素加到总和中
  • 当总和达到或超过目标时，尝试移动左指针来缩小窗口，并更新最小长度
class Solution:
    def minSubArrayLen(self, target, nums):
        min_ = float("inf")              # 初始化最小数组长度为无穷大
        sum = 0
        l = 0
        for r in range(len(nums)):
            sum += nums[r]              # 扩展窗口，增加当前元素到总和
            while sum >= target:        # 当总和达到或超过目标时，尝试收缩窗口
                min_ = min(min_, r - l + 1)   # 更新最小长度
                sum -= nums[l]                # 从总和中减去左侧元素
                l += 1

        return min_ if min_ != float("inf") else 0

print( Solution().minSubArrayLen(7, [2, 3, 1, 2, 4, 3]) )  # 输出 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 106.最小覆盖子串

  • 76.最小覆盖子串 (opens new window)
  • 给你两个个字符串 s 、 t ，返回 s 中涵盖 t 所有字符的最小子串
  • 如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 ""
输入：s = "ADOBECODEBANC", t = "ABC"   输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'

输入: s = "a", t = "aa"    输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，因此没有符合条件的子字符串，返回空字符串
1
2
3
4
5

1、Python

  • 字典初始化：dic_t 记录 t 中每个字符的数量，dic_s 记录当前窗口中字符的数量
  • 初始化：min_len 用于记录最小窗口的长度，ans_l 和 ans_r 用于记录最小窗口的左右边界
  • check 函数：检查当前窗口是否包含 t 中所有的字符
  • 滑动窗口：右指针 r 扩展窗口，左指针 l 收缩窗口，更新 dic_s 和检查窗口是否符合要求

class Solution:
    def minWindow(self, s, t):
        dic_s = {}       # 用于记录当前窗口中字符的数量
        dic_t = {}       # 记录t现次数：t = "ABC", dic_t = {'A': 1, 'B': 1, 'C': 1}
        min_len = float('inf')             # 最小窗口长度为正无穷
        ans_l, ans_r = -1, -1              # 答案 左、右指针

        for c in t:
            dic_t[c] = dic_t.get(c, 0) + 1

        def check():                         # 检查当前窗口是否包含 t 中的所有字符
            for k, v in dic_t.items():
                if dic_s.get(k, 0) < v:
                    return False
            return True

        l = 0
        for r in range(len(s)):
            if s[r] in dic_t:                    # 如果 s[r] 是 t 中的字符
                dic_s[s[r]] = dic_s.get(s[r], 0) + 1

            while check() and l <= r:            # 如果当前窗口包含 t 中的所有字符，尝试收缩窗口
                if r - l + 1 < min_len:          # 更新最小窗口的长度和位置
                    min_len = r - l + 1
                    ans_l, ans_r = l, r

                if s[l] in dic_t:                # 移动左指针，更新窗口中的字符数量
                    dic_s[s[l]] -= 1
                l += 1

        if ans_l == -1:        # 没有找到返回 ""
            return ""
        return s[ans_l:ans_r+1]

print(Solution().minWindow("ADOBECODEBANC", "ABC"))  # 输出 "BANC"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# 107.最接近的三数之和

  • 16.最接近的三数之和 (opens new window)
  • 给你一个长度为 n 的整数数组 nums 和 一个目标值 target请你从 nums 中选出三个整数，使它们的和与 target 最接近
  • 返回这三个数的和，假定每组输入只存在恰好一个解
输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2)
1
2
3

1、Python

  • 使用一个循环遍历数组，选定一个基准数 nums[i]
  • l 和 r分别指向剩余部分的最左边和最右边的元素
  • 如果当前和更接近目标值，则更新最接近的和
  • 如果当前和小于目标值 l += 1,如果当前和大于目标值r -= 1 循环完成即可找到最接近
class Solution:
    def threeSumClosest(self, nums, target):
        nums.sort()
        sum = float('inf')              # 初始化一个变量用于存储最接近的三数之和
        for i in range(len(nums) - 2):  # 保证i最大能到达倒数第三个位置
            l, r = i + 1, len(nums) - 1
            while l < r:                # 移动左右指针来寻找最接近的三数之和
                tmp_sum = nums[i] + nums[l] + nums[r]  # 计算当前三数之和
                if abs(tmp_sum - target) < abs(sum - target):  # 如果当前和更接近目标值，则更新最接近的和
                    sum = tmp_sum

                if tmp_sum == target:  # 如果当前和正好等于目标值，直接返回
                    return tmp_sum
                elif tmp_sum < target: # 如果当前和小于目标值，说明需要更大的数，将左指针右移
                    l += 1
                else:                  # 如果当前和大于目标值，说明需要更小的数，将右指针左移
                    r -= 1

        return sum        # 返回找到的最接近的三数之和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

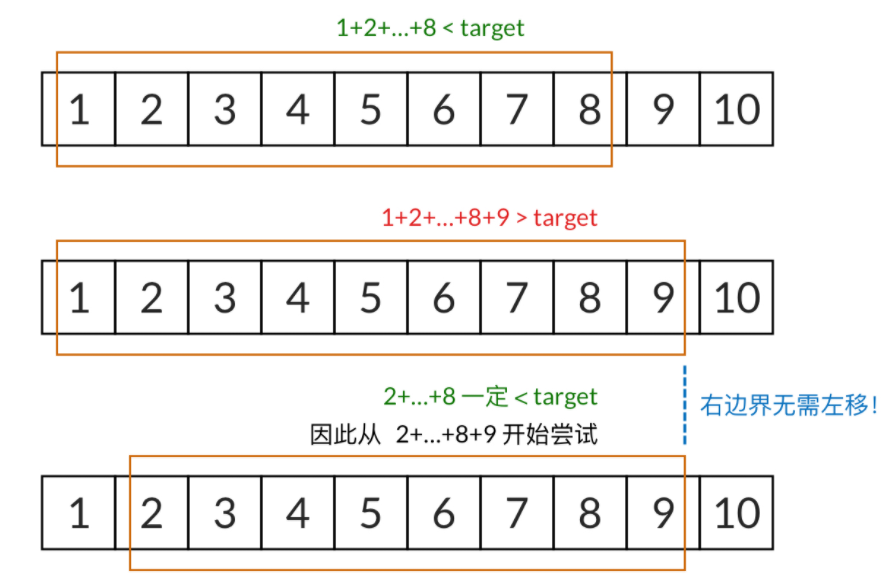
# 108.和为s的连续正数序列

  • 和为s的连续正数序 (opens new window) 被移除了
  • 输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）
  • 序列内的数字由小到大排列，不同序列按照首个数字从小到大排列
输入：target = 9
输出：[[2,3,4],[4,5]]
输入：target = 15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]
1
2
3
4

1、Python 滑动窗口

  • 双指针滑动窗口: 使用两个指针 left 和 right，分别表示序列的起点和终点

  • 移动指针: 通过调整 left 和 right 来改变当前序列的和，如果序列和小于 target，则右

def findNum(target):
    l, r = 1, 2   # 初始化两个指针，分别指向序列的起始位置和结束位置
    sum = l + r   # 初始化当前窗口的和
    res = []      # 用于存储符合条件的结果序列
    while l < r:     # 当左指针小于右指针时继续循环
        if sum == target:
            # 如果当前序列的和等于目标值，将序列加入结果集
            res.append(list(range(l, r + 1)))
            sum -= l     # 移动左指针，同时更新序列的和
            l += 1
        elif sum < target:
            r += 1      # 如果当前序列的和小于目标值，移动右指针增加序列和
            sum += r
        else:
            sum -= l    # 如果当前序列的和大于目标值，移动左指针减少序列和
            l += 1
    return res

print(findNum(9))   # 输出: [[2, 3, 4], [4, 5]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 109.滑动窗口最大值

1、Python

  • 使用list模仿队列，存储元素值倒序排列（存的是索引）

    • eg: q = [1,2,3]       # 实际值是 [3, -1, -3]
      1

  • r 指针不断滑动，加入新元素与队尾最小元素比对

  • 如果r指针新元素比队尾元素大，就一直pop()出队，直到队列为空或者遇到比当前元素大的值

  • 然后将当前元素加入队列，移除不在当前窗口范围内的元素，记录窗口最大值

class Solution:
    def maxSlidingWindow(self, nums, k):
        res = []
        q = []           # 保持q中元素值倒序排列（存的是索引）用队列其实更好
        l = 0
        for r in range(len(nums)):
            while q and nums[q[-1]] < nums[r]: # 如果当前值大于栈顶元素就出栈
                q.pop()
            q.append(r)     # 当前值 小于等于 栈顶值时 入栈（索引）

            if q[0] < l:    # 移除不在当前窗口范围内的元素
                q.pop(0)

            if r >= k - 1:  # 当窗口达到大小 k 时，记录最大值
                res.append(nums[q[0]])
                l += 1      # 窗口左边界右移

        return res

print(Solution().maxSlidingWindow([1, 3, -1, -3, 5, 3, 6, 7], 3))  # [3, 3, 5, 5, 6, 7]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#

# ② 排序与搜索

# 201.合并两个有序数组

  • 88.合并两个有序数组 (opens new window)

  • 给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中*，*使 nums1 成为一个有序数组

  • 初始化 nums1 和 nums2 的元素数量分别为 m 和 n

  • 你可以假设 nums1 的空间大小等于 m + n，这样它就有足够的空间保存来自 nums2 的元素

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
1
2

1、Python

  • 将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中
  • 我们为两个数组分别设置一个指针p1 与 p2 来作为队列的头部指针

class Solution:
    def merge(self, nums1, m, nums2, n):
        p1, p2, p = m - 1, n - 1, len(nums1) - 1

        # `从后往前` 遍历，比较 nums1[p1] 和 nums2[p2]，把较大值放入 nums1[p]
        while p1 >= 0 and p2 >= 0:
            if nums1[p1] > nums2[p2]:  # nums1 当前元素较大
                nums1[p] = nums1[p1]   # 把 nums1[p1] 放到 nums1[p]
                p1 -= 1
            else:       # nums2 当前元素较大
                nums1[p] = nums2[p2]   # 把 nums2[p2] 放到 nums1[p]
                p2 -= 1
            p -= 1  # 每次放入一个元素后，p 向前移动

        # 如果 nums2 还有剩余元素（p2 >= 0），说明 nums1 剩余部分已经正确，只需拷贝 nums2 剩余部分
        nums1[:p2 + 1] = nums2[:p2 + 1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 202.旋转数组的最小数字

  • 154.寻找旋转排序数组中的最小值 II (opens new window)

  • 已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组

  • 例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：

    • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
    • 若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]

  • 数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]]

1、Python

  • 左边界为low，右边界为high，区间的中点为 m,被分为下面三情况
    • 如果 m的值小于 R的值，最小值一定在左半部分
    • 如果m的值大于R的值，最小值一定在右半部分
    • 如果中间值m等于 R的值，那么右指针就向左移动一位
class Solution:
    def findMin(self, nums):
        # 左边界为L，右边界为R，区间的中点为 m
        L, R = 0, len(nums) - 1
        while L < R:
            m = L + (R - L) // 2
            if nums[m] < nums[R]:  # 如果 m的值小于 R的值，最小值一定在左半部分
                R = m
            elif nums[m] > nums[R]:  # 如果m的值大于R的值，最小值一定在右半部分
                L = m + 1
            else:  # 如果中间值m等于 R的值，那么右指针就向左移动一位
                R -= 1  # R右指针向左移动，值是会变小的
        return nums[L]
1
2
3
4
5
6
7
8
9
10
11
12
13

2、Go

func minArray(numbers []int) int {
  // 左边界为L，右边界为R，区间的中点为 m
	L, R := 0, len(numbers) - 1
	for L < R {
		m := L + (R-L) / 2
		if numbers[m] < numbers[R] {  // 如果 m的值小于 R的值，最小值一定在左半部分
			R = m
		} else if numbers[m] > numbers[R] {  // 如果m的值大于R的值，最小值一定在右半部分
			L = m + 1
		} else {  // 如果中间值m等于 R的值，那么右指针就向左移动一位
			R -= 1  // R右指针向左移动，值是会变小的
		}
	}
	return numbers[L]
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 203.寻找峰值

  • 162.寻找峰值 (opens new window)

  • 给你一个整数数组 nums，找到峰值元素并返回其索引

  • 数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可

  • 你可以假设 nums[-1] = nums[n] = -∞

  • 你必须实现时间复杂度为 O(log n) 的算法来解决此问题

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2
 	   或者返回索引 5， 其峰值元素为 6
1
2
3
4
  • 要解决这个问题，我们可以使用二分查找来达到 O(log n) 的时间复杂度
  • 由于题目中提到我们可以假设 nums[-1] = -∞ 和 nums[n] = -∞
  • 这意味着数组两端的元素比其外部的元素都要大，因此至少存在一个峰值

1、Python

  • 我们用二分查找不断缩小搜索区间，每次都根据 nums[mid] 和 nums[mid + 1] 的大小关系决定是缩小到左侧还是右侧

  • 当 left == right 时，我们找到了一个峰值所在的位置

class Solution:
    def findPeakElement(self, nums):
        l, r = 0, len(nums) - 1
        while l < r:
            mid = (l + r) // 2
            # 如果中间元素大于其右侧的元素，则峰值在左侧
            if nums[mid] > nums[mid + 1]:
                r = mid
            else:
                # 如果中间元素小于等于其右侧的元素，则峰值在右侧
                l = mid + 1
        return l
1
2
3
4
5
6
7
8
9
10
11
12

# 204.搜索旋转排序数组

  • 33.搜索旋转排序数组 (opens new window)

  • 整数数组 nums 按升序排列，数组中的值 互不相同

  • nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转

  • 给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的索引，否则返回 -1

原始数组：[0,1,2,4,5,6,7]  
旋 转 后：[4,5,6,7,0,1,2]
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4
1
2
3
4

1、Python

  • 可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的

def search(nums, target):
    if not nums:
        return -1
    l, r = 0, len(nums) - 1
    while l <= r:
        mid = (l + r) // 2
        if nums[mid] == target:
            return mid

        if nums[0] <= nums[mid]:  # 如果 第一个元素 < 中间值 证明前半部分有序
            # 如果目标元素 在前半部分，就移动右指针为 mid-1
            if nums[0] <= target < nums[mid]:
                r = mid - 1
            else:  # 否则移动左指针 为 mid+1
                l = mid + 1
        else:   # 否则 后半部分有序
            # 如果目标元素 在后半部分，就移动左指针为 mid+1
            # 判断后半部分是否有序，需要比较目标值 target 与 数组最后一个元素
            if nums[mid] < target <= nums[len(nums) - 1]:
                l = mid + 1
            else: # 否则右指针为 mid - 1
                r = mid - 1
    return -1

print( search([4,5,6,7,0,1,2], 0) )  # 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 205.数组中的第K个最大元素

例：寻找第二大元素
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
1
2
3

22.1 python

  • 实现类似快速排序的分区过程，但只继续处理可能包含第 k 大元素的那部分数组

    • 每次选择数组的第一个元素作为基准点，将数组分为两部分，左边部分大于基准，右边部分小于基准

    • 通过递归，缩小查找范围，直到找到第 k 大的元素

    • 注：这里是倒序排列，所以第k大的数就是left == k - 1时

class Solution:
    def findKthLargest(self, nums, k):
        def partition(low, high):
            l, r = low, high
            p = nums[l]         # 选择最左边的数作为基准
            while l < r:
                while l < r and nums[r] <= p:
                    r -= 1
                nums[l] = nums[r]  # 右侧较大值填充左侧空位

                while l < r and nums[l] > p:
                    l += 1
                nums[r] = nums[l]  # 左侧较小值填充右侧空位

            nums[l] = p  # l == r, p 的最终位置确定
            return l     # 返回 pivot 的最终索引

        def quick_select(low, high):
            idx = partition(low, high)  # idx左侧都比自己小，右侧都比自己大

            if idx == k - 1:   # 如果基准的最终位置是第 k 大的位置，找到，直接返回
                return nums[idx]
            elif idx > k - 1:  # 如果基准位置大于第 k 大的位置，证明 k 一定在左边
                return quick_select(low, idx - 1)
            else:              # 如果基准位置小于第 k 大的位置，继续从右边找
                return quick_select(idx + 1, high)

        return quick_select(0, len(nums) - 1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 206.合并区间

  • 56.合并区间 (opens new window)

  • 以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi]

  • 请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]
1
2
3

1、Python

  • 首先，我们将列表中的区间按照左端点升序排序
  • 相邻两个列表如果前一个列表最大值小于下一个列表最小值，肯定无需合并，直接添加到空列表
  • 否则找到这两个列表中的最大值，拓展区间
def merge(intervals):
    intervals.sort(key=lambda x: x[0])  # 首先，我们将列表中的区间按照左端点升序排序
    res = []
    for interval in intervals:
        # 如果列表为空，或者 一个列表右边的值 < 下一个列表左边的元素
        if not res or res[-1][1] < interval[0]:
            res.append(interval)  # 直接添加，无需合并
        else:
            # 否则的话，我们就可以与上一区间进行合并, 右边值为两个列表右侧较大的值
            res[-1][1] = max(res[-1][1], interval[1])

    return res

print(merge([[2,3],[1,6],[8,10],[15,18]]))  # [[1, 6], [8, 10], [15, 18]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 207.寻找两个正序数组的中位数

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
1
2
3
4
5
6
7

1、Python

  • 我们可以把问题转化为寻找两个数组中的第 k 小的元素
  • 对于两个数组 nums1 和 nums2，如果我们可以找到第 k 小的元素，那么中位数的计算就可以分为两种情况

    • 如果两个数组的总长度是奇数，那么中位数就是第 (m+n)//2 + 1 个元素

    • 如果两个数组的总长度是偶数，那么中位数就是第 (m+n)//2 和第 (m+n)//2 + 1 个元素的平均值

class Solution:
    def findMedianSortedArrays(self, nums1, nums2):
        def findKth(arr1, arr2, k):   # 找到两个排序数组中第 k 小的元素
            if len(arr1) > len(arr2): # 保证 arr1 是较短的数组
                return findKth(arr2, arr1, k)
            if not arr1:
                return arr2[k - 1]

            if k == 1:
                return min(arr1[0], arr2[0])

            # 二分查找：我们取两个数组的前 k//2 个元素 和 数组长度比较 取小值（避免越界）
            i = min(len(arr1), k // 2)
            j = min(len(arr2), k // 2)
            
            # arr2 的前 j 个元素不可能是第 k 小的元素,忽略掉 arr2 的前 j 个元素
            if arr1[i - 1] > arr2[j - 1]:       
                return findKth(arr1, arr2[j:], k - j)
            else:  # arr1 的前 i 个元素不可能是第 k 小的元素忽略掉 arr1 的前 i 个元素
                return findKth(arr1[i:], arr2, k - i)

        total_len = len(nums1) + len(nums2)

        # 如果总长度是奇数，中位数就是第 (total_length // 2 + 1) 小的元素
        if total_len % 2 == 1:         
            return findKth(nums1, nums2, total_len // 2 + 1)
        else:  # 总长度偶数，中位数是 total_length//2 和 total_length//2 + 1 小的元素的平均值
            return (
               findKth(nums1, nums2, total_len // 2) +
               findKth(nums1, nums2, total_len // 2 + 1)
            ) / 2.0

print(Solution().findMedianSortedArrays([1, 2], [3, 4]))  # 输出: 2.5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 208.前 K 个高频元素

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
1
2

1、Python

  • 使用快排 查找前k大数，然后只对这些数排序
from collections import Counter

class Solution:
    def topKFrequent(self, nums, k):
        dic_cnt = Counter(nums)       # 统计每个元素的频率 {1: 3, 2: 2, 3: 1}
        arrs = list(dic_cnt.items())  # 将频率转换为 [(1, 3), (2, 2), (3, 1)]

        def quick_select(low, high, k):
            p = arrs[low][1]          # 选择最左边的数作为基准
            l, r = low, high

            while l < r:
                while l < r and arrs[r][1] <= p:
                    r -= 1
                if l < r:
                    arrs[l] = arrs[r]

                while l < r and arrs[l][1] > p:
                    l += 1
                if l < r:
                    arrs[r] = arrs[l]

            arrs[l] = (arrs[l][0], p)  # l == r, p 的最终位置确定

            if l == k - 1:     # 如果基准的最终位置是第 k 大的位置，找到，直接返回
                return
            elif l > k - 1:    # 如果基准位置大于第 k 大的位置，证明k一定在左边
                quick_select(low, l - 1, k)
            else:              # 如果基准位置小于第 k 大的位置，继续从右边找
                quick_select(l + 1, high, k)

        quick_select(0, len(arrs) - 1, k)      # 快速选择前 k 个高频元素
        return [arrs[i][0] for i in range(k)]  # 打印前k个 [(1, 3), (2, 2), (3, 1)]

print(Solution().topKFrequent( [1, 1, 1, 2, 2, 3], 2))  # 输出: [1, 2]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# 209.在排序数组中查找元素的第一个和最后一个位置

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]
1
2

1、Python

class Solution:
    def searchRange(self, nums, target):
        def find_pos(nums, target, is_first):
            l, r = 0, len(nums) - 1
            pos = -1                   # position 位置
            while l <= r:
                mid = l + (r - l) // 2
                if nums[mid] == target:
                    pos = mid
                    if is_first:
                        r = mid - 1    # 查找第一个位置，继续向左
                    else:
                        l = mid + 1    # 查找最后一个位置，继续向右
                elif nums[mid] < target:
                    l = mid + 1
                else:
                    r = mid - 1
            return pos

        first_pos = find_pos(nums, target, True)
        last_pos = find_pos(nums, target, False)
        return [first_pos, last_pos]

print(Solution().searchRange([5, 7, 7, 8, 8, 10], 8))  # 输出: [3, 4]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#

# ③ 子数组问题

# 301.最大子数组和

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6
1
2
3

1、Python

  • 基本思路就是遍历一遍，用两个变量，一个记录最大的和，一个记录当前的和

  • 如果当前和小于0，当前最长序列到此为止以该元素为起点继续找最大子序列

  • 时空复杂度貌似还不错......（时间复杂度 O(n)，空间复杂度 O(l)

def maxSub(nums):
	max_ = nums[0]  # 假设第一个为最大和
	for i in range(1, len(nums)):
		if nums[i - 1] > 0:  # 如果当前和大于0就将当前和加上当新数据，否则重新开始当前和
			nums[i] += nums[i - 1]
		max_ = max(max_, nums[i])  # 当前和 于 记录最大和比较，大的为新的最大和
	return max_

print(maxSub([-2,1,-3,4,-1,2,1,-5,4]))  #  6 ==》[4,-1,2,1]
1
2
3
4
5
6
7
8
9

2、Go

  • 基本思路就是遍历一遍，一个记录最大的和，一个记录当前的和

  • 如果当前的和大于0，就继续加下一个元素，然后比较max，如果更大就更新max

  • 时空复杂度貌似还不错......（时间复杂度 O(n)，空间复杂度 O(l)

func maxSubArray(nums []int) int {
	max := nums[0]  // 假设第一个为最大和
	for i := 1; i < len(nums); i++ {
		if nums[i] + nums[i-1] > nums[i] {   // 如果nums[i-1]当前和大于0，将当前和加上当新数据，否则重新开始当前和
			nums[i] += nums[i-1]
		}
		if nums[i] > max {  // 当前和与记录最大的和比较，如果当前和更大就更新
			max = nums[i]
		}
	}
	return max
}
1
2
3
4
5
6
7
8
9
10
11
12

# 302.乘积最大子数组

  • 152.乘积最大子数组 (opens new window)

  • 给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组

  • （该子数组中至少包含一个数字），并返回该子数组所对应的乘积

输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6
1
2
3

1、Python

  • 由于负数的存在，子数组中存在偶数个负数可以变成正数
  • 以 数组 nums = [2, 3, -2, 4]为例
class Solution:
    def maxProduct(self, nums):
        max_ = min_ = res = nums[0]  # 最大乘积、最小乘积（防止负数影响），最终结果
        for i in range(1, len(nums)):
            # 如果当前数为负数，则交换 max_ 和 min_，因为负数可能翻转最大最小值
            if nums[i] < 0:
                max_, min_ = min_, max_

            max_ = max(nums[i], nums[i] * max_) #本身 或 乘以最大乘积
            min_ = min(nums[i], nums[i] * min_) # 本身 或 乘以最大乘积（负数情况）
            res = max(res, max_)  # res 记录全局最大乘积

        return res

print(Solution().maxProduct([-2, 3, 2, -4]))  # 输出 48
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

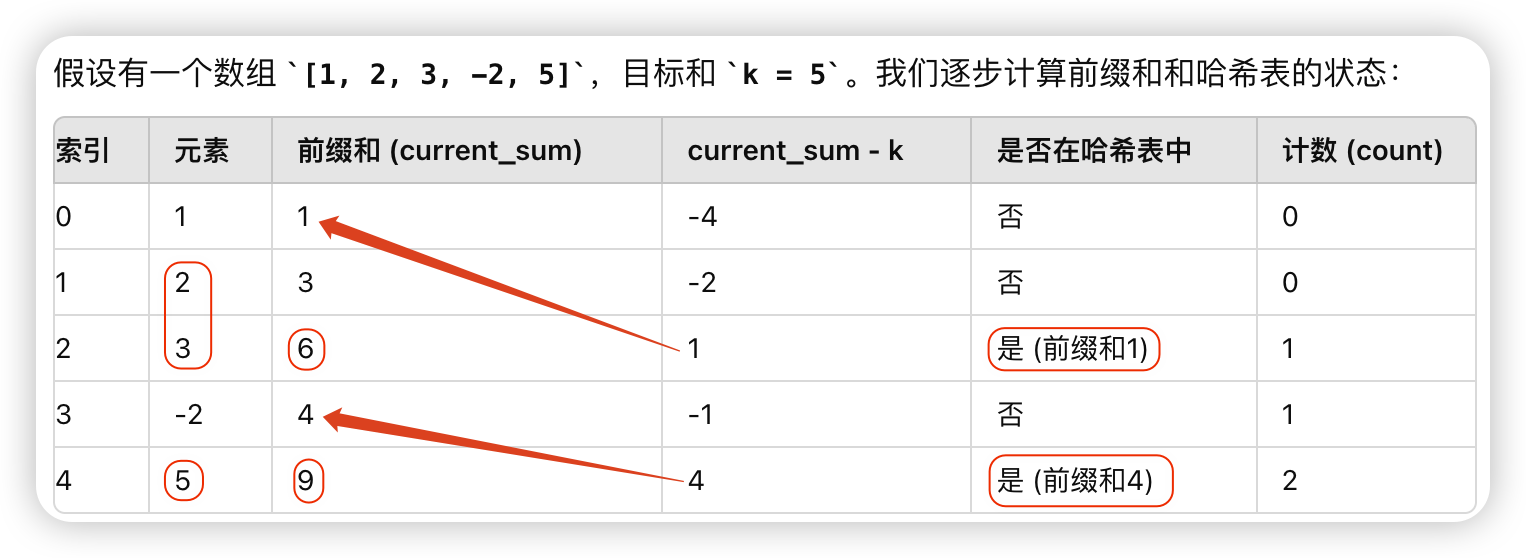
# 303.和为 K 的子数组

输入：nums = [1,2,3], k = 3
输出：2  # 1,2 和 3 两种
1
2

1、Python

  • 前缀和是指从数组的开始位置到当前位置所有元素的累积和
  • 使用前缀和，可以将一个子数组的和转换为前缀和之间的差值，从而更高效地判断是否存在某个和为 k 的子数组
class Solution:
    def subarraySum(self, nums, k):                                                                                                                                                                                           
        dic = {0: 1}         # 字典记录前缀和出现的次数，表示前缀和为0的子数组出现过1次
        sum, res = 0, 0    # 当前的前缀和, 和为k的子数组的数量
        for i in nums:
            sum += i         # 更新当前的前缀和
            if sum - k in dic:   # 如果 (当前前缀和 - k) 在哈希表中，说明 存在 和为 k 的子数组
                res += dic[sum - k]
            dic[sum] = dic.get(sum, 0) + 1  # 将当前的前缀和记录到哈希表中

        print(dic)  # {0: 1, 1: 1, 3: 1, 6: 1, 4: 1, 9: 1}
        return res

print(Solution().subarraySum([1,2,3,-2,5], 5) )  # [2,3]   [5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14

上次更新: 2025/3/25 17:29:52
01.数组
06.回溯算法

← 06.回溯算法→

最近更新
01
08.动态规划
03-25
02
06.回溯算法
03-25
03
05.手写数字识别
03-13
更多文章>
Theme by Vdoing | Copyright © 2019-2025 逍遥子 技术博客 京ICP备2021005373号