03.神经网络概述

# 01.神经网络

定义：模拟生物神经网络的数学模型，通过多层非线性变换学习复杂模式

# 1、神经网络类型

类型	结构特点	应用场景
前馈神经网络（FNN）	单向传播，无循环结构	手写数字识别（MNIST）
卷积神经网络（CNN）	卷积层提取局部特征，池化层降维	图像分类（ResNet）、目标检测（YOLO）
循环神经网络（RNN）	循环结构处理序列数据，存在梯度消失问题	文本生成、股票预测
Transformer	自注意力机制（Self-Attention）并行处理长序列	机器翻译（BERT、GPT）

# 2、深度学习关键技术

Dropout：
- 随机丢弃神经元，防止过拟合
- 示例：训练时以50%概率关闭神经元，测试时使用全部
批量归一化（Batch Norm）：
- 标准化每层输入，加速训练
- 公式： x' = (x - μ)/σ * γ + β（γ、β为可学习参数）
迁移学习：
- 复用预训练模型（如ImageNet上的CNN），微调最后一层
- 示例：用VGG16模型快速训练医学图像分类器

# 02.核心组件

# 1、神经网络

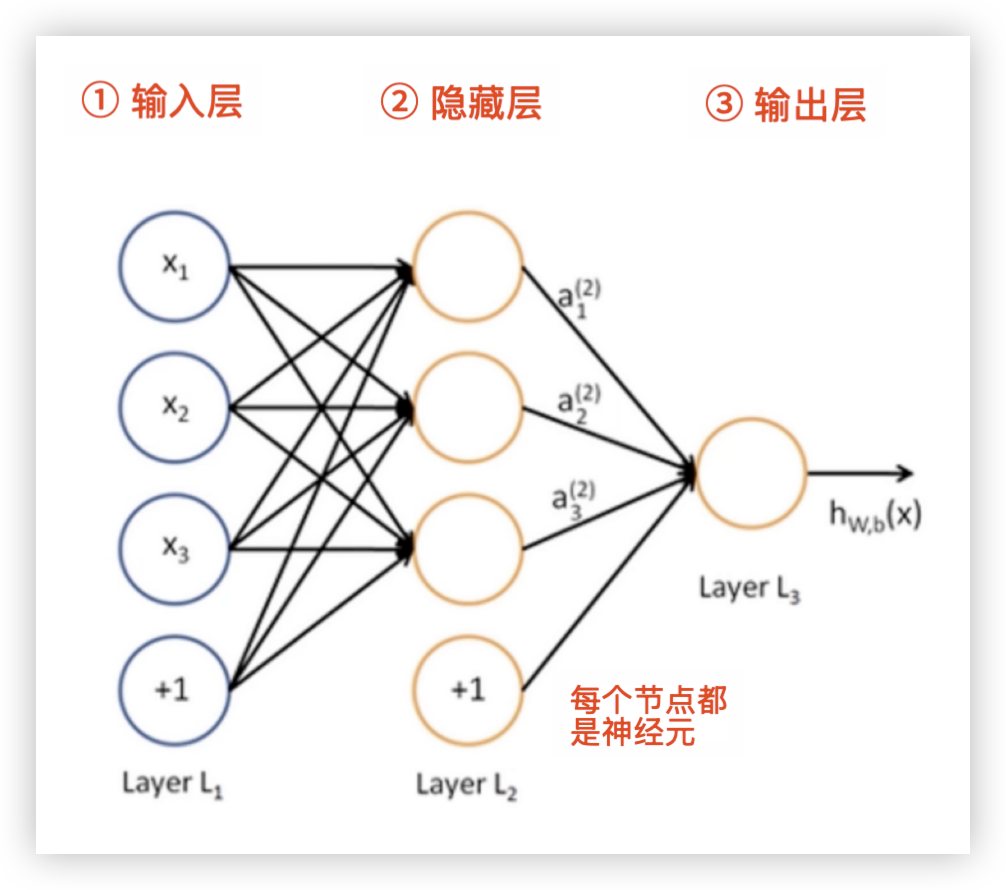
神经网络如下图所示：输入层、输出层、隐藏层、多层感知器

输入层：接收外部数据作为输入
隐藏层：处理输入数据，提取特征，进行复杂的转换
输出层：生成最终的预测结果或分类结果
神经元：每个神经元接收上一层的输入，进行加权求和、加偏置并通过激活函数产生输出
层与层的关系：
- 每一层的输出作为下一层的输入，每层对输入数据进行非线性转换，最终得到输出层的结果

# 2、感知器

# `1）感知器`

感知器是神经网络中最基本的单层神经网络模型
它由一个输入层、一个神经元（或多个神经元）和一个输出层组成
它用于二分类任务，其中输入的每个特征都会与相应的权重相乘
求和后通过一个阶跃函数（Heaviside 函数）得到输出
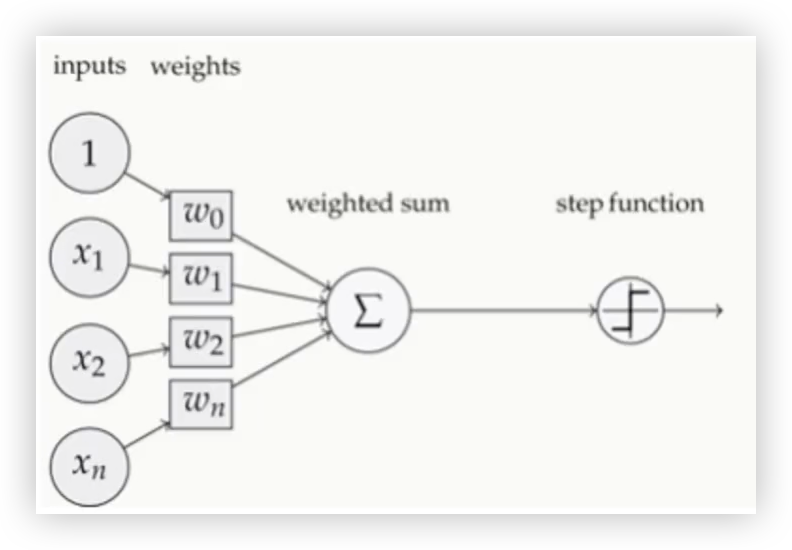
下图就是一个感知器
- 1,x1,x2,x3是输入，w0,w1,w2,w3是权值
- f 是一个激活函数 z = f(w1⋅x1 + w2⋅x2 + w3⋅x3 + b)
- 根据输入，权值，激活函数计算出下一级输出可以理解为就是一个感知器

# `2）激活函数`

假设有一个神经元，接收到三个输入信号 x1,x2,x3，对应的权重分别是 w1,w2,w3，偏置为 b
神经元的输出 y 可以表示为：z = f(w1⋅x1 + w2⋅x2 + w3⋅x3 + b)
其中，f 是一个激活函数（例如 ReLU、Sigmoid 等）
激活函数的作用
- 激活函数的作用就是将神经元的加权求和结果 z 转换为输出值
- 这是神经元能够“激活”的关键步骤
- 具体来说，激活函数决定了感知器的输出为哪个类别
阶跃函数 (Step Function)
- 在感知器中，常用的激活函数是阶跃函数，它的输出只有两种情况
- 如果加权求和的结果 z 大于或等于 0，输出为 1；否则，输出为 0
假设我们有一个感知器，用于判断某个物品是否应该被归类为“接受”或“拒绝”
它接收两个输入特征：
- x1 = 3（表示物品的价格）
- x2 = 1（表示物品的质量）
权重分别为
- w1 = 0.5
- w2 = 0.8
偏置 b=−1，那么加权求和的结果是
- z = f(w1⋅x1 + w2⋅x2 + w3⋅x3 + b)
- z = 0.5⋅3 + 0.8⋅1 − 1 = 1.5 + 0.8 − 1 = 1.3
然后通过 阶跃函数 计算输出f(1.3)=1 因此，感知器输出为 1，表示“接受”

# 3、前向传播

前提条件：必须知道输入项值

前向传播是神经网络从输入数据逐步生成预测结果的核心流程，其核心作用包括

信息传递：将输入数据逐层映射到输出层，最终得到预测值（如分类概率、回归值）

非线性建模：通过激活函数引入非线性，使网络能够拟合复杂函数（如分类边界、曲线趋势）

参数依赖：显式建立输入特征与参数（权重、偏置）的数学关系，为反向传播提供计算路径

# 0）概述

从输入层到隐藏层，再到输出层，数据在网络中依次传播
每一层根据输入计算输出，并将其传递给下一层，直到最终得到输出层的结果
这个计算的过程就被称为前向传播
线性变换的基本形式z = Wx + b
- 下标的1,2,3代表该层的第i个神经元（unit）
- 上标的[1],[2]等代表当前是第几层
- y^代表模型的输出，y才是真实值，也就是标签
- 上图中的x1，x2，x3 不是代表4个样本！而是一个样本的四个特征（4个维度的值）

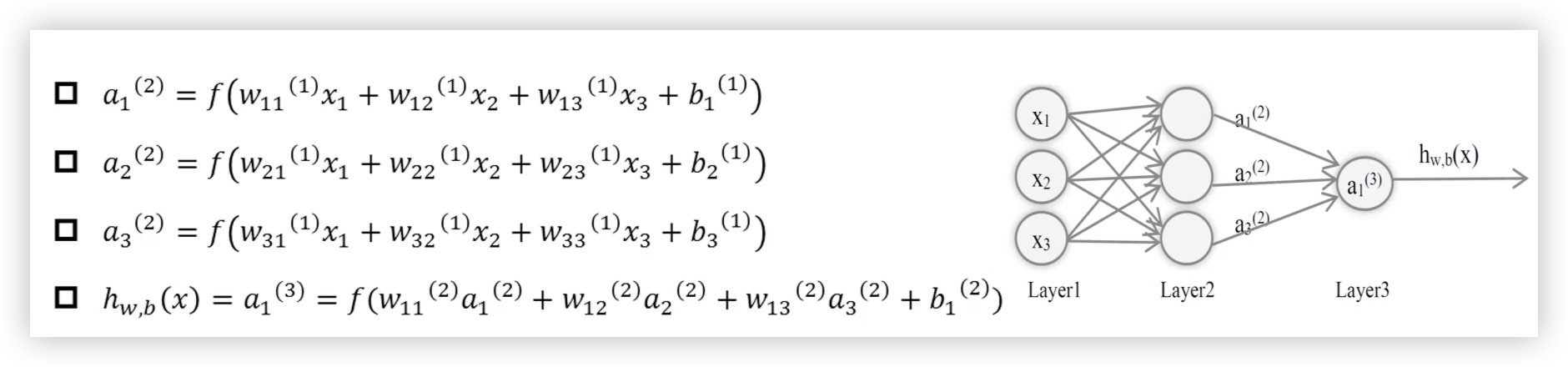
前向传播是神经网络训练的第一步，它的核心目标是从输入数据逐层计算神经网络的输出（预测值）
前向传播涉及 线性变换、激活函数、损失计算 这些重要概念

# 1）线性变换

概述
- 线性变换是指神经元的输入是前一层神经元的加权和，再加上偏置
- 这个过程可以看作矩阵乘法，它决定了神经元的加权输入
- 线性变换的基本形式z = Wx + b
- 权重 W 和偏置 b 共同决定输入 x 如何被映射到下一层的表示
作用
- 将输入特征的线性组合转化为“预激活值”（z），赋予不同特征权重
- 如 w1=0.5 表示学习时间对结果的正向贡献，w2=-0.2 表示睡眠时间可能的负面影响
选择依据
- 权重意义：
  - 权重 W 表示特征的重要性，正负号体现贡献方向，绝对值大小体现影响强度
  - 例如，案例中未标准化的数据直接赋予权重，需依赖后续优化调整（如反向传播）
- 偏置作用：
  - 偏置 b 为模型提供灵活性，允许在特征全为零时仍有输出
  - 如 b=0.1 表示即使学习时间和睡眠时间均为零，仍有基础通过概率
- 线性局限性：
  - 单纯线性变换只能建模线性关系，需激活函数引入非线性

# 2）激活函数

Sigmoid（适用于二分类问题）
使输出值映射到 (0,1) 之间，适用于概率预测

ReLU（适用于深度网络）
只保留正值，解决梯度消失问题

Tanh（双曲正切）
使输出值映射到 (−1,1) 之间，适用于零均值数据

Softmax（多分类问题）
用于多分类任务，归一化为概率分布

激活函数作用
- 将线性输出 z 映射到特定范围（如 [0, 1]），使其具有概率意义
- 案例中将 z=0.5 映射为 62.2%，表示“通过考试”的概率。
选择依据
- 输出范围：Sigmoid 的输出范围 [0, 1] 天然适合二分类概率（如通过/不通过）
- 梯度特性：
  - Sigmoid 的导数 σ'(z) = σ(z)(1-σ(z)) 便于梯度计算
  - 如反向传播中直接使用 a^L 和 y 计算误差
- 替代方案：
  - 多分类问题用 Softmax（输出概率和为1）
  - 隐藏层常用 ReLU（缓解梯度消失，加速训练）

# 3）损失函数

损失函数衡量预测值和真实值之间的误差
均方误差（MSE）（适用于回归）

交叉熵损失（Cross-Entropy Loss）

Softmax + 交叉熵

作用
- 量化预测概率与真实标签的差异
- 案例中真实标签为 y=1（通过考试），交叉熵损失衡量预测概率 a=0.622 的误差
- 公式及计算
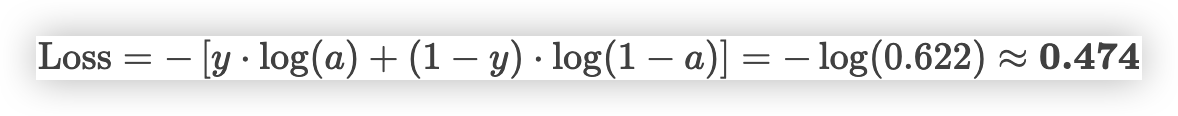
选择依据：
- 概率匹配：
  - 交叉熵直接衡量两个概率分布（预测分布 vs 真实分布）的差异，与 Sigmoid 输出的概率天然匹配
- 梯度友好：
  - 交叉熵的梯度仅与误差 (a - y) 相关，避免了 Sigmoid 导数中 a(1-a) 的数值衰减
  - 如均方误差的梯度会因 a(1-a) 而缩小，导致训练缓慢

# 4）案例

定义输入和参数
- 输入数据（特征）：x = [2, 3]表示某学生学习了 2 小时，睡眠 3 小时
- 权重：w = [0.5, -0.2] 学习时间对结果有正向贡献，睡眠时间权重为负（假设数据未标准化）
- 偏置：b = 0.1
① 线性变换 z=Wx+b （加权和）
- 将输入与权重相乘后求和，加上偏置
- z= (x₁⋅w₁) + (x₂⋅w₂) + b = (2⋅0.5) + (3⋅−0.2) + 0.1 = 0.5
② 激活函数（Sigmoid）
- 将线性变换结果映射到 [0, 1]，表示概率
- 模型预测该学生通过考试的概率为 62.2%
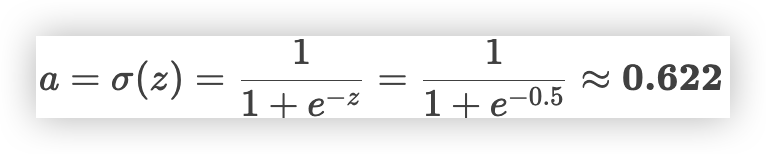
③ 损失计算（交叉熵）
- 衡量预测值与真实值的差距
- 假设真实标签是 y = 1（实际通过了），用交叉熵衡量预测误差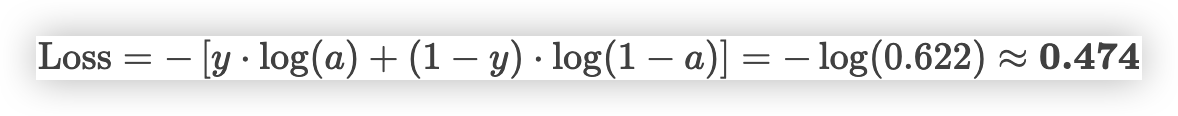

# 4、反向传播BP

# 1）概述

反向传播（Backpropagation）是用于计算梯度的一种算法

其核心目标是计算损失函数 $L$ 对模型参数（如权重 $W$ 和偏置 $b$）的偏导数

这样，才能利用梯度下降等优化算法更新参数，使损失函数逐步减小，提高模型的学习效果

反向传播是用于计算梯度的一种算法，目标是计算损失函数对各个参数（w和b）的梯度
其核心目标是计算损失函数 $L$ 对模型参数（如权重 $W$ 和偏置 $b$）的偏导数
以便通过梯度下降更新参数，通过计算输出层结果与真实值之间的偏差来进行逐层调节参数
这样，才能利用梯度下降等优化算法更新参数，使损失函数逐步减小，提高模型的学习效果
反向传播公式 L 损失函数，权重 $W$ 和偏置 $b$

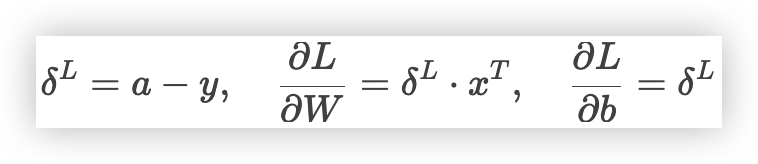
梯度计算高效且直观，与任务目标（如分类概率）直接关联
通过参数更新，模型逐步修正权重和偏置，使预测值逼近真实标签

# 2）反向传播目标

反向传播的核心目标

# 3）推导

以下结合前向传播案例
- 输入 x=[2,3]，权重 W=[0.5,−0.2]，偏置b=0.1
- 输出概率 a=0.622，真实标签 y=1，交叉熵损失 L≈0.474
计算输出层误差（链式法则起点）

上次更新: 2025/3/13 17:01:28

← 02.Tensor 张量 04.房价预测→

03.神经网络概述

# 01.神经网络

# 1、神经网络类型

# 2、深度学习关键技术

# 02.核心组件

# 1、神经网络

# 2、感知器

# 1）感知器

# 2）激活函数

# 3、前向传播

# 0）概述

# 1）线性变换

# 2）激活函数

# 3）损失函数

# 4）案例

# 4、反向传播BP

# 1）概述

# 2）反向传播目标

# 3）推导

# `1）感知器`

# `2）激活函数`