01.基础数学

# 基础数学

线性代数
- 矩阵和向量的运算（加法、乘法、转置、点积）
- 矩阵分解（如特征值分解、奇异值分解）
- 张量的概念（PyTorch 的核心数据结构）
微积分
- 导数和偏导数
- 链式法则（用于理解反向传播）
- 梯度概念
概率与统计
- 概率分布（如正态分布、均匀分布）
- 期望、方差、协方差
- 最大似然估计
优化理论
- 损失函数
- 梯度下降法及其变种（如 SGD、Adam）
- 学习率调整

# 01.线性代数

线性代数：矩阵乘法、向量运算（神经网络的参数通常以矩阵形式存储）
线性代数是深度学习和神经网络中非常重要的数学基础
因为神经网络中的许多操作（如前向传播、反向传播、权重更新等）都可以通过矩阵和向量运算来高效地表示

# 1、矩阵乘法

矩阵乘法是线性代数中非常基本的操作，它广泛用于神经网络中，用来表示层与层之间的输入输出关系
在神经网络中，矩阵乘法用来将输入数据与权重矩阵相乘，从而计算每一层的输出
矩阵乘法规则
假设你有两个矩阵A 和 B，如果 A 是一个 m×n 的矩阵
B是一个 n×p 的矩阵，那么它们的乘积 C=A×B 将是一个 m×p 的矩阵
具体来说，矩阵 C 的每一个元素 Cij是 A的第 i 行与 B的第 j 列的点积

# 2、向量运算

向量是线性代数中的基本对象，它可以表示神经网络中的输入数据、权重、偏置等
向量与矩阵的乘法
- 在神经网络中，输入数据通常是一个向量，权重是一个矩阵
- 通过矩阵和向量的乘法，可以得到该层的输出

# 3、神经网络中应用

在神经网络中，输入数据通常以矩阵或向量的形式存储，而网络的权重也是以矩阵形式存储
网络的每一层的输出可以通过矩阵与向量的乘法来计算
输入层到隐藏层的计算：输入数据与权重矩阵相乘，然后加上偏置，最后通过激活函数进行非线性变换
输出层的计算：最后一层的输出通常是一个向量，表示神经网络的预测结果
例如，在一个简单的前馈神经网络中
- 假设输入是一个向量 x，权重矩阵是 W，偏置是 b，激活函数是 σ（sigma）
- 那么隐藏层的输出可以表示为h = σ( W × x + b)

# 02.微积分

微积分：理解链式法则（Chain Rule），梯度（导数）的概念

# 1、导数、偏导数、梯度

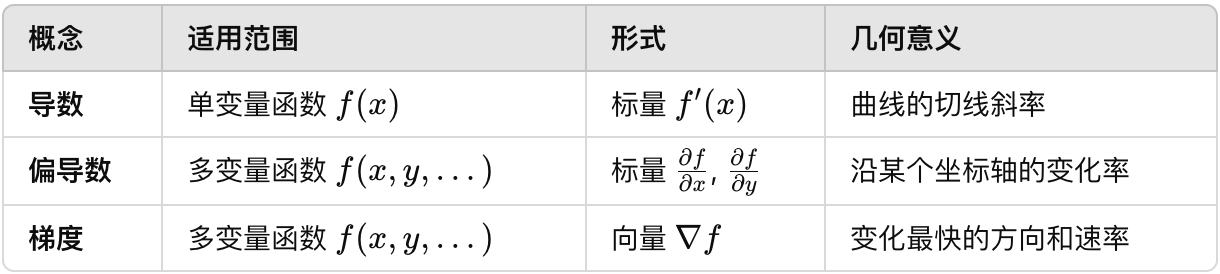
# 1）导数

导数是函数变化率的度量，描述的是函数在某一点附近的瞬时变化率
对于单变量函数f(x)，导数定义为：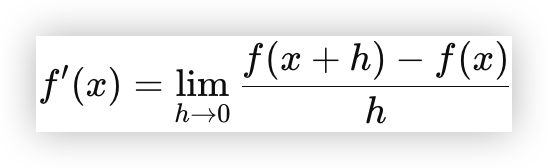
- 直观上，导数表示函数曲线在某点的 切线斜率。
- 如果 f'(x) > 0，函数在该点是递增的
- 如果 f'(x) < 0，函数在该点是递减的
- 如果 f'(x) = 0，可能是极值点或拐点
在数学上，导数就是函数在某一点的瞬时变化率
如果你有一个函数 f(x)，那么它在某一点 x = a 处的导数（即梯度）可以告诉你，随着 x 变化时，f(x) 变化的速度
例如，函数 f(x) = x^2 的导数是 f'(x) = 2x，它表示当 x 增加时，函数 f(x) 变化的速率

# 2）偏导数

当函数涉及多个变量时，我们通常研究它对其中某一个变量的变化率，而保持其他变量不变（这就是偏导数）
假设你有一个多变量函数 f(x1,x2,…,xn)，这个函数依赖于多个变量（x1,x2,…,xn）
那么，就表示 f对第 i 个变量 xi 的偏导数
偏导数的意义可以从 "一维方向上的变化" 来理解
对于多变量函数来说，我们不可能一次性考虑所有变量的变化，而是固定其他变量，只研究某个特定变量对函数的影响

# 3）梯度

梯度是多变量函数偏导数的向量化表示，表示函数在某点变化最快的方向及变化率大小
梯度定义：多变量函数f(x1,x2, …. xn)，梯度是一个向量，定义为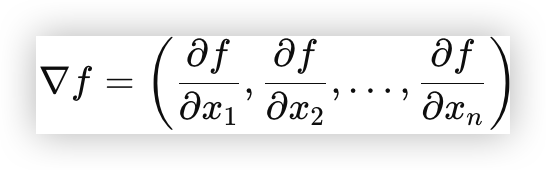
计算示例

# 2、链式法则

链式法则用于计算复合函数的导数 公式为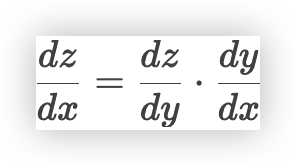
复合函数是由多个函数嵌套在一起构成的，比如 f(g(x))，其中 f 和 g 都是函数
链式法则告诉我们，如果想计算 f(g(x)) 的导数
- 可以通过先计算 g(x) 的导数
- 再计算 f 对 g(x) 的导数，然后将两者相乘
现在，我们通过例子 y=2x, z=y**2 , 求 dz/dx 来详细解释链式法则的应用
- 内层函数 g(x) 对应 y=2x
- 外层函数 f(g) 对应 z=y**2

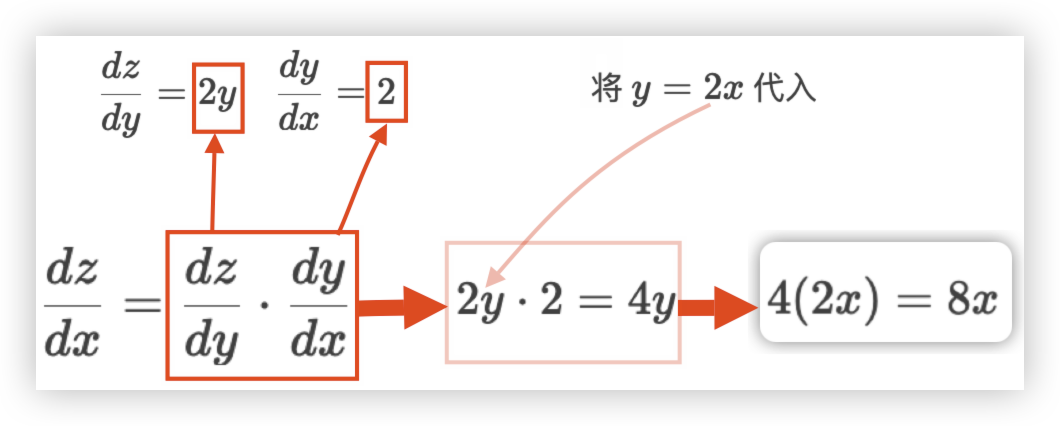
# 03.概率与统计

# 1、均值、方差和分布

均值（也称作期望值或数学期望）是数据的中心位置，表示一组数值的平均值
方差描述数据的分散程度，衡量数据与均值之间的偏离程度
分布描述数据在不同值上的可能性，即数据或随机变量的取值模式

# 2、最大似然估计（MLE）

最大似然估计（MLE）：与损失函数（如交叉熵）的联系

# 04.优化理论

# 1、梯度下降法

bilibili (opens new window)

基本优化理论：梯度下降法（Gradient Descent）的目标是找到损失函数的最小值

梯度下降法是优化理论中的一个核心算法，广泛应用于机器学习和深度学习中，用于优化模型的参数，最小化损失函数

它的目标是通过逐步调整参数，朝着损失函数的最小值方向移动，从而获得模型的最佳参数

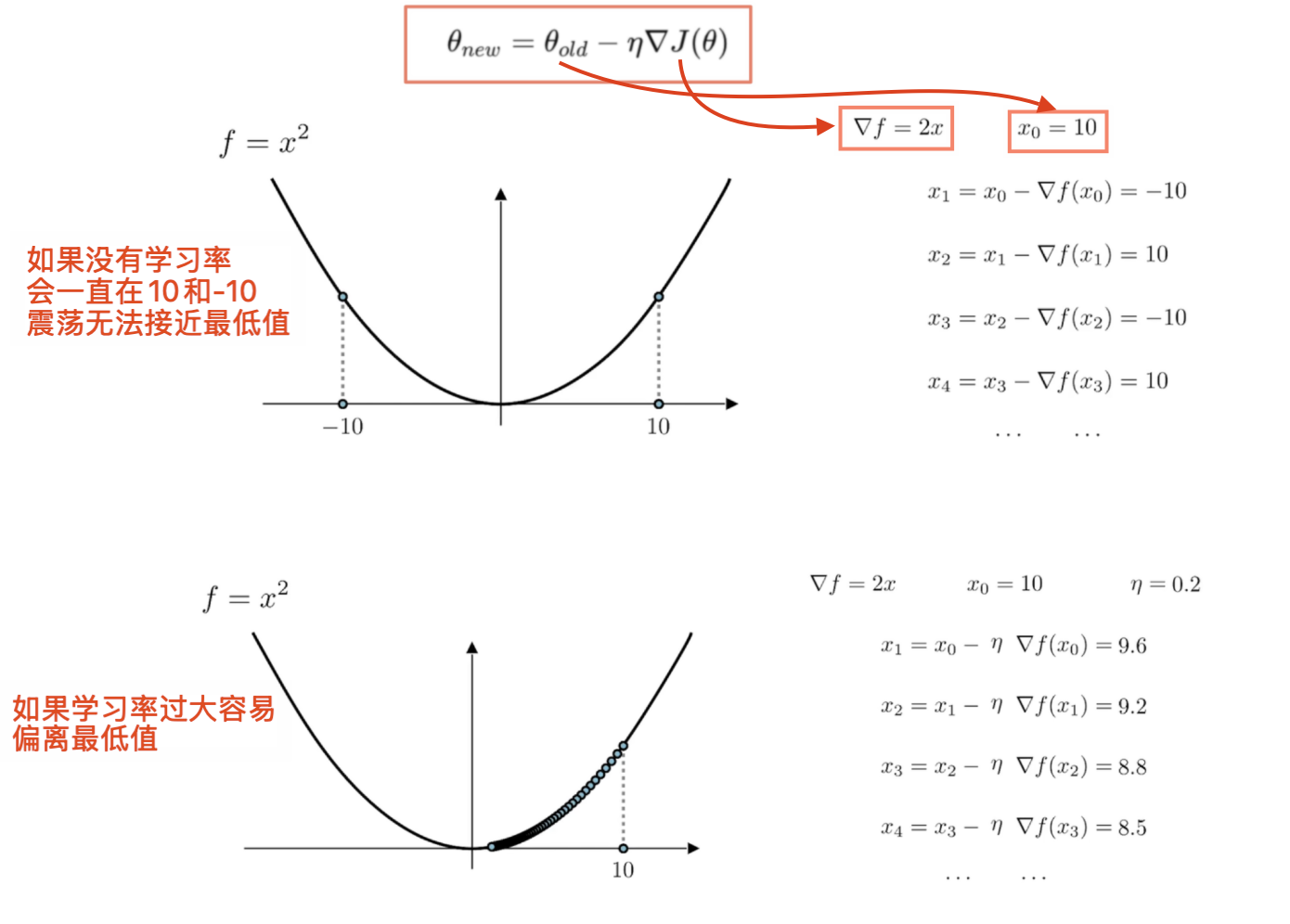
# 1）梯度下降法

梯度下降法的核心公式就是
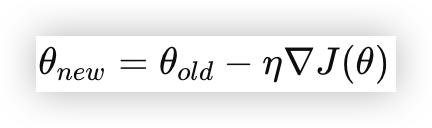
关键部分包括 损失函数、梯度、学习率和更新规则
例：我们的损失函数就是 f(x)=x^2 ，因为我们希望找到 x的最优值，使得f(x)达到最小值

# 2）学习率

学习率过大：
- 如果学习率 η 过大，更新步伐会太大
- 可能导致模型的参数在损失函数的最小值附近“跳跃”，甚至可能完全错过最优解，或者不收敛
学习率接近0：
- 如果学习率 η 过小，每次更新的步长会非常小，意味着每次调整的幅度非常小
- 模型的参数几乎不再改变，收敛速度极慢，甚至在很长的时间内也无法达到理想的最小值
终止条件
- 虽然学习率接近0不是直接的终止条件，但它通常表明算法已经陷入停滞，无法有效继续优化
- 这时可以认为梯度下降已经基本收敛
计算梯度：求出损失函数 L 对参数 W 和 b的偏导数

上次更新: 2025/3/13 17:01:28

10.损失函数→