01.顺时针打印矩阵

• 顺时针打印矩阵 (opens new window)

输入：
matrix = 
[
    [1,2,3],
    [4,5,6],
    [7,8,9]
]
输出：[1,2,3,6,9,8,7,4,5]

1、python

• 参考 (opens new window)

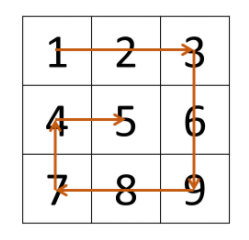
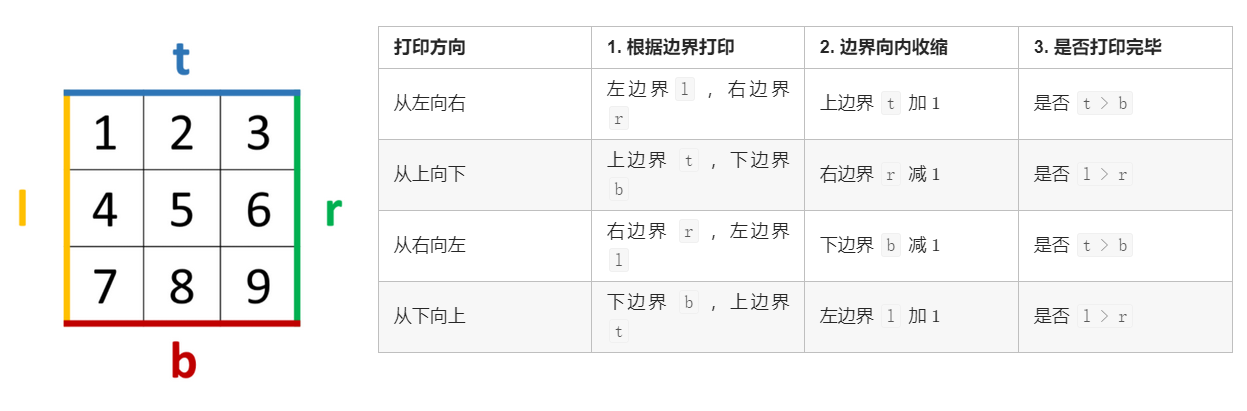
• 顺时针打印矩阵的顺序是 “从左向右、从上向下、从右向左、从下向上” 循环。

• 因此，考虑设定矩阵的“左、上、右、下”四个边界，模拟以上矩阵遍历顺序。

• 初始化： 矩阵 左、右、上、下 四个边界 l , r , t , b ，用于打印的结果列表 res 。

• 循环打印： “从左向右、从上向下、从右向左、从下向上” 四个方向循环，每个方向打印中做以下三件事 （各方向的具体信息见下表） ；

  • 根据边界打印，即将元素按顺序添加至列表 res 尾部；
  • 边界向内收缩 1（代表已被打印）；
  • 判断是否打印完毕（边界是否相遇），若打印完毕则跳出。
  • 返回值： 返回 res 即可。

def matrixOrder(matrix):
    if not matrix: return []
    # 左、右、上、下 四个边界 l , r , t , b ，用于打印的结果列表 res
    l, r, t, b, res = 0, len(matrix[0]) - 1, 0, len(matrix) - 1, []
    while True:
        for i in range(l, r + 1): res.append(matrix[t][i])  # left to right
        t += 1                      # 从左往右的下一步是往下走，上边界内缩，故t+1
        if t > b: break
        for i in range(t, b + 1): res.append(matrix[i][r])  # top to bottom
        r -= 1                      # 从上往下的下一步是从右往左，右边界收缩，r-1
        if l > r: break
        for i in range(r, l - 1, -1): res.append(matrix[b][i])  # right to left
        b -= 1                      # 从右往左的下一步是从下往上，下边界收缩，b-1
        if t > b: break
        for i in range(b, t - 1, -1): res.append(matrix[i][l])  # bottom to top
        l += 1                      # 从下到上的下一步是从左到右，左边界收缩，l+1
        if l > r: break
    return res

if __name__ == '__main__':
    matrix = [
        [1,2,3],
        [4,5,6],
        [7,8,9]
    ]
    print( matrixOrder(matrix) )  # [1, 2, 3, 6, 9, 8, 7, 4, 5]

02.旋转图像

• 48.旋转图像 (opens new window)

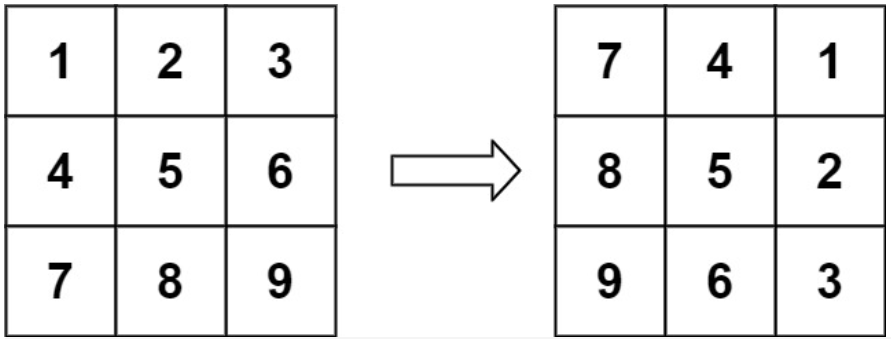
• 给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

• 你必须在** 原地 (opens new window)** 旋转图像，这意味着你需要直接修改输入的二维矩阵。

• 请不要 使用另一个矩阵来旋转图像

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

1、python

def trans90(matrix):
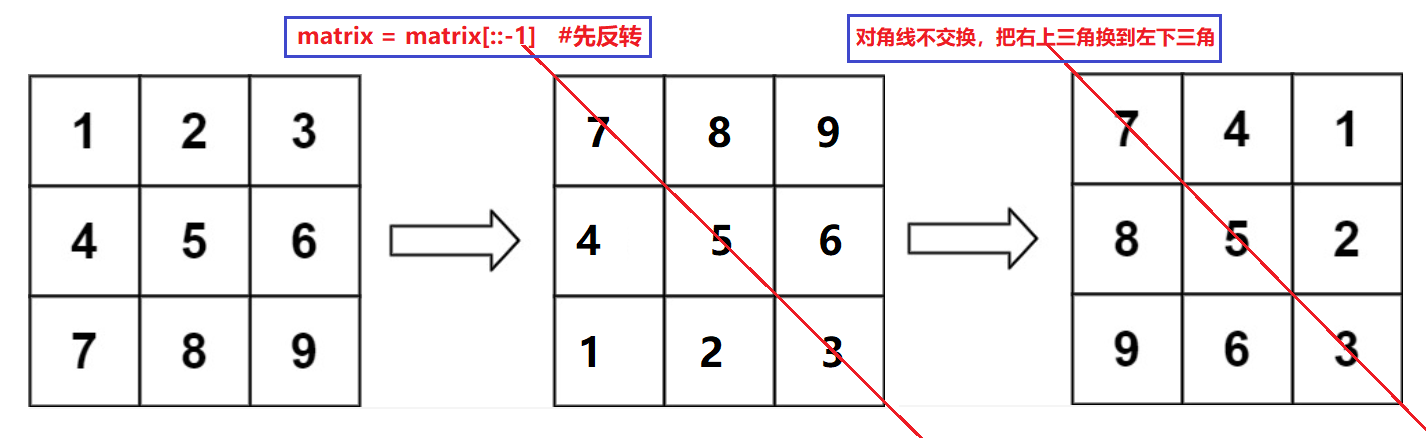
    matrix = matrix[::-1]   # 先反转 # [[7, 8, 9], [4, 5, 6], [1, 2, 3]]
    rows,cols = len(matrix),len(matrix[0])
    for i in range(rows):   # 做转置，对角线不交换，把右上三角换到左下三角
        for j in range(i,cols):   # 注意从i开始，不要换了又把左下三角换回去了
            if i==j:
                continue
            else:
                matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]
    return matrix

if __name__ == "__main__":
    matrix = [[1,2,3],[4,5,6],[7,8,9]]
    print( trans90(matrix) )   # [[7, 4, 1], [8, 5, 2], [9, 6, 3]]

03.单词搜索

• 79.单词搜索 (opens new window)

• 给定一个二维网格和一个单词，找出该单词是否存在于网格中

• 单词必须按照字母顺序，通过相邻的单元格内的字母构成

• 其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。

• 同一个单元格内的字母不允许被重复使用。

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false

1、python

• 使用深度优先搜索（DFS）和回溯的思想实现。

• 关于判断元素是否使用过，我用了一个二维数组 mark 对使用过的元素做标记。

• 外层：遍历

  • 首先遍历 board 的所有元素，先找到和 word 第一个字母相同的元素，然后进入递归流程
  • 假设这个元素的坐标为 (i, j)，进入递归流程前，先记得把该元素打上使用过的标记

• 内层：递归

  • 好了，打完标记了，现在我们进入了递归流程。递归流程主要做了这么几件事：
  • 从 (i, j) 出发，朝它的上下左右试探，看看它周边的这四个元素是否能匹配 word 的下一个字母
  • 如果匹配到了：带着该元素继续进入下一个递归
  • 如果都匹配不到：返回 False
  • 当 word 的所有字母都完成匹配后，整个流程返回 True

class Solution:
    directs = [(0, 1), (0, -1), (1, 0), (-1, 0)]  # 定义上下左右四个行走方向

    def exist(self, board, word):
        n = len(board[0])  # 获取二维网格 长
        m = len(board)  # 获取二维网格 宽
        # 定义一个二维数组 `mark` 对使用过的元素做标记
        mark = [[0 for _ in range(n)] for _ in range(m)]

        for i in range(m):
            for j in range(n):
                if board[i][j] == word[0]:
                    mark[i][j] = 1      # 将该元素标记为已使用
                    if self.backtrack(i, j, mark, board, word[1:]) == True:
                        return True
                    else:
                        mark[i][j] = 0  # 回溯
        return False

    def backtrack(self, i, j, mark, board, word):
        if len(word) == 0:
            return True

        for direct in self.directs:
            cur_i = i + direct[0]
            cur_j = j + direct[1]

            if cur_i >= 0 \
                    and cur_i < len(board) \
                    and cur_j >= 0 and cur_j < len(board[0]) \
                    and board[cur_i][cur_j] == word[0]:

                if mark[cur_i][cur_j] == 1:  # 如果是已经使用过的元素，忽略
                    continue
                mark[cur_i][cur_j] = 1  # 将该元素标记为已使用
                if self.backtrack(cur_i, cur_j, mark, board, word[1:]) == True:
                    return True
                else:
                    mark[cur_i][cur_j] = 0  # 回溯
        return False


board = [
    ['A', 'B', 'C', 'E'],
    ['S', 'F', 'C', 'S'],
    ['A', 'D', 'E', 'E']
]
print(Solution().exist(board, "ABCCED"))  # True
print(Solution().exist(board, "SEE"))     # True
print(Solution().exist(board, "ABCB"))    # False