不做大哥好多年
xiaonaiqiang
2025-03-11
目录

04.房价预测

# 01.房价预测

  • 回归问题：使用13种特征，构建模型，推算第14中特征，房价

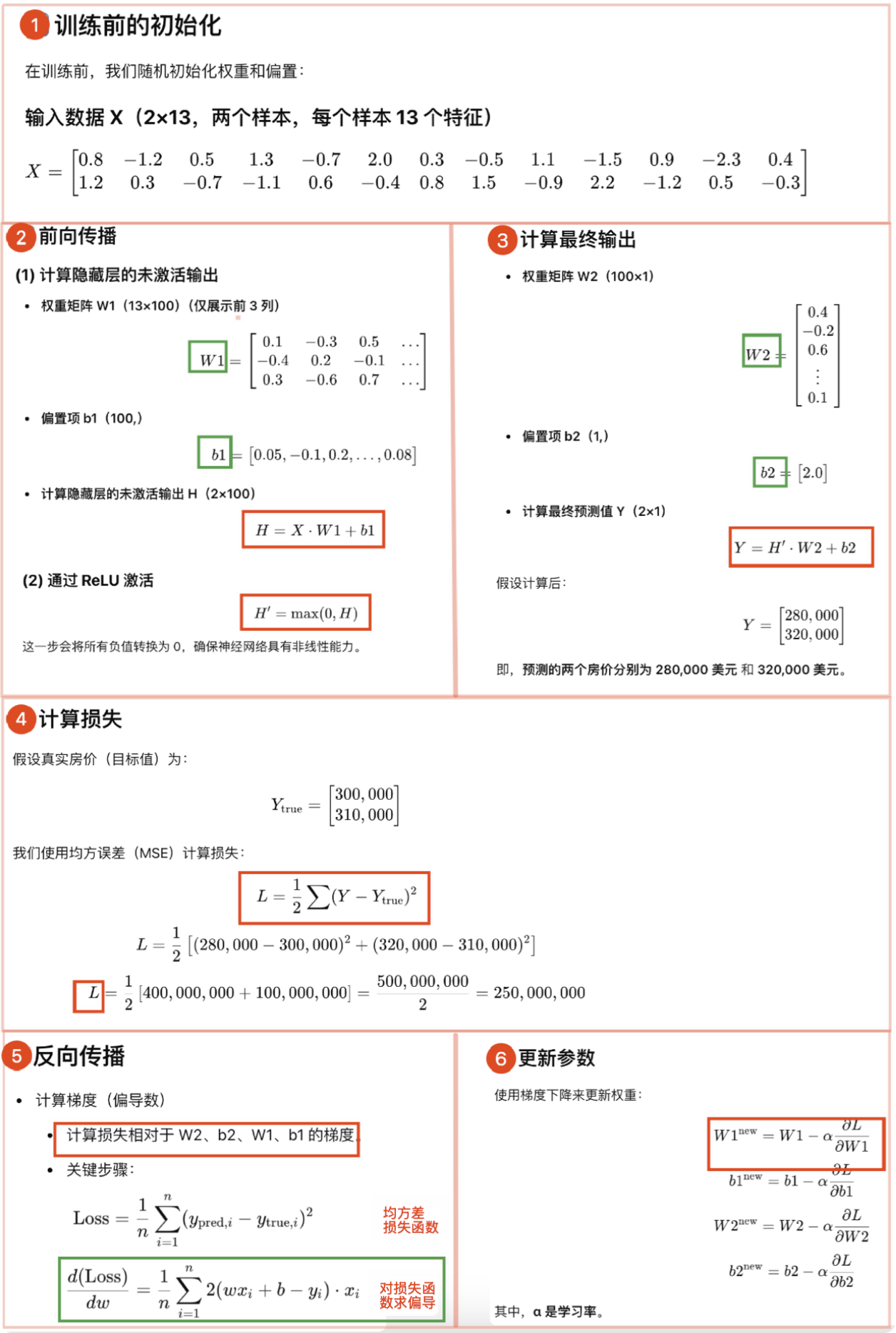
# 1、训练过程

  • 计算损失
    • 由于是回归问题，常用 均方误差（MSE） 作为损失函数
  • 反向传播
    • 自动计算梯度（torch.autograd），更新参数（如 W1, b1, W2, b2）
    • 训练过程的实质就是优化模型参数（例如权重 w），使得损失函数 L 最小化
    • θ = θ − η∇L（对应PyTorch 代码中 w = w - a * w.grad）
      • 其中 η 是学习率，∇L 是损失函数关于参数的梯度
  • 迭代优化
    • 使用优化器（如 torch.optim.Adam）不断调整参数，直到损失收敛，模型可以准确预测房价

# 2、房价预测代码

import torch
import numpy as np
import re

# 1. 数据加载与处理
ff = open("/Users/tom/work_pytorch/pytorch_code/04/cls_reg/housing.data").readlines()
data = []
for item in ff:
    out = re.sub(r"\s{2,}", " ", item).strip()
    data.append(out.split(" "))
data = np.array(data, dtype=float)
Y = data[:, -1]  # Y 是房价（目标变量）
X = data[:, 0:-1]  # X 是房屋的 13 个特征（输入变量）


# 2. 训练集与测试集划分
# 取数据的前 496 行作为训练集，后面的数据作为测试集
X_train = X[0:496, ...]
Y_train = Y[0:496, ...]
X_test = X[496:, ...]
Y_test = Y[496:, ...]


# 3. 构建神经网络
'''
Net 是一个神经网络类，继承自 torch.nn.Module。
该网络包含：
    输入层：接收 13 个特征变量（如房屋面积、房龄等）
    隐藏层：100 个神经元，并使用 ReLU 作为激活函数
    输出层：1 个神经元，用于预测房价
torch.nn.Linear(n_feature, 100) 创建线性层
torch.relu() 作为非线性激活函数，使网络具备更强的表达能力
'''


class Net(torch.nn.Module):
    def __init__(self, n_feature, n_output):
        """
        :param n_feature: 输入特征的数量 13（eg:房屋面积、位置...）
        :param n_output: 将 100 维隐藏层的输出压缩到 n_output 维（房价预测通常是 n_output=1）
        """
        super(Net, self).__init__()
        # 隐藏层：根据输入特征数量 (13) 来生成一个 (100, 13) 形状的权重矩阵 W1
        self.hidden = torch.nn.Linear(n_feature, 100)
        # 输出层：将 100 维隐藏层的输出压缩到 n_output 维（房价预测通常是 n_output=1）
        self.predict = torch.nn.Linear(100, n_output)

    def forward(self, x):
        # 第二: 前向传播
        out = self.hidden(x)     # 线性变换: H = W1 * X + b
        out = torch.relu(out)    # 非线性激活: H'=max(0,H)
        # 第三: 计算房价预测值
        out = self.predict(out)  # 输出层 预测价格: Y = H' * W2 + b2
        return out


net = Net(13, 1)  # 13 个输入特征，1 个输出（房价）


# 4. 损失函数与优化器
loss_func = torch.nn.MSELoss()  # 均方误差损失
# 梯度下降优化:  W = W − α⋅ ∂MSE/∂W
# α 是学习率（lr=0.01）  （∂MSE/∂W）是损失函数对权重的梯度
optimizer = torch.optim.Adam(net.parameters(), lr=0.01)


# 5. 训练过程
for i in range(10000):
    # 第一: 训练前数据
    x_data = torch.tensor(X_train, dtype=torch.float32)  # 13 个特征（输入变量）
    y_data = torch.tensor(Y_train, dtype=torch.float32)  # 房价（目标变量）
    pred = net.forward(x_data)  # 前向传播（得到房价预测值）Y = H' * W2 + b2
    pred = torch.squeeze(pred)  # 去掉形状为1的维度 [496, 1] 变形为 [496]

    # 第四: 计算损失
    # 计算损失（真实房价和预测房价） 乘 0.001 是为了 缩小损失值，避免梯度过大导致训练不稳定
    loss = loss_func(pred, y_data) * 0.001
    optimizer.zero_grad()  # 清空梯度，否则梯度会错误叠加

    # 第五: 反向传播
    # 反向传播 作用是计算损失函数（Loss）对每个神经网络参数的梯度
    # dL/dW1 = (y'-y)**2求导
    # 这些梯度将用于 optimizer.step() 更新参数，使模型在训练过程中不断优化
    loss.backward()

    # 第六: 更新参数
    # optimizer.step() 使用loss.backward()求导结果，计算新的W和b
    # eg: W.grad =>  w1'=w1 - η * dL/dW1
    optimizer.step()

    print("ite:{}, loss_train:{}".format(i, loss))
    print(pred[0:10])  # 打印前 10 个预测值
    print(y_data[0:10])  # 打印前 10 个真实值

    # 最后可以简单 测试集评估（这部分不是训练过程，只是检验当前模型预测准确度）
    x_data = torch.tensor(X_test, dtype=torch.float32)
    y_data = torch.tensor(Y_test, dtype=torch.float32)
    pred = net.forward(x_data)  # 前向传播（得到房价预测值）
    pred = torch.squeeze(pred)  # 去掉形状为1的维度 [496, 1] 变形为 [496]
    loss_test = loss_func(pred, y_data) * 0.001
    print("ite:{}, loss_test:{}".format(i, loss_test))

# torch.save(net, "model/model.pkl")
# torch.load("")
# torch.save(net.state_dict(), "params.pkl")
# net.load_state_dict("")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

# 3、预测原理

  • 房价预测属于回归问题，即给定一些房屋的特征，预测其价格
  • 训练过程的实质就是优化模型参数（例如权重 w），使得损失函数 L 最小化
  • 输入层（13 个特征） → 隐藏层（100 维，ReLU） → 输出层（1 个房价预测值）

  • 神经网络是通用逼近器

    • 神经网络本质上是一个非线性函数逼近器，可以学习数据的复杂映射关系
    • 即使房价与输入特征之间的关系复杂，神经网络可以通过学习权重参数 W 和 b 来找到合适的函数逼近

  • 输入层

  • n_feature 代表房屋的特征（房龄、房屋面积等13个特征）

# 1）隐藏层

隐藏层 H=XW1+b1

  • self.hidden = torch.nn.Linear(n_feature, 100)  # n_feature 代表房屋的特征（房屋面积、位置...）
    1

  • 该层执行线性变换: H=XW1+b1

  • 由于 100 个神经元，可以学习输入特征的复杂模式和交互关系

  • 矩阵乘法

    • X 形状：(N, 13) (N个样本，每个样本有13个特征)

    • W1 形状：(13, 100) (随机生成的13行 100列矩阵)

    • 乘法结果：(N, 100)（N 个样本，每个样本生成 100 维隐藏层表示）

  • 深度学习中，随机初始化 W1 有多种策略，后续在做深入探究

  • 当你定义 self.hidden = torch.nn.Linear(n_feature, 100) 时

  • 包含一个权重矩阵 W1 (nfeature x 100矩阵 ) 和一个偏置 b1 (形状：100,)

  • 计算梯度时，直接计算整个矩阵的梯度，形状同 W1

  • 同一个 batch 内的所有样本会共享一个梯度 W.grad，但这个梯度实际上是所有样本梯度的均值

为什么要用 W1 (13 × 100) 进行特征转换？

  • 学习数据中的复杂关系
    • 13 个特征可能不是线性相关的，房价可能由多个特征的组合影响，比如 房屋面积+地理位置 可能比单独考虑面积更重要
    • 通过 增加隐藏层维度（100 维），让神经网络有更多参数去学习这些复杂关系
  • 高维空间的表达能力更强
    • 13 维输入可能不足以描述数据的完整信息
    • 100 维隐藏层可以让网络有更多的自由度 来表达数据的模式，捕捉更多的特征组合

# 2）激活函数

  • ReLU 激活函数 H′=max(0,H)
  • # 即正数保留，负数修正为0
out = torch.relu(out)  # ReLU(x)=max(0,x)
    1
    2

  • ① 引入非线性

    • 神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值
    • 如果不用激活函数，无论神经网络有多少层，输出都是输入的线性组合
    • ReLU 激活函数可以使结果不再是输入的线性组合，可以逼近任意函数

  • ② 防止梯度消失，提高训练效率

    • ReLU 在输入大于 0 时，梯度恒为 1，不会消失，有助于梯度传播，加快收敛

  • ③ 稀疏性

    • ReLU(x) = max(0, x) 会将一部分神经元的输出变为 0，使得模型更稀疏（部分神经元不参与计算）
    • 这种稀疏性能减少计算量，提高训练效率，同时具有一定的正则化效果，防止过拟合

# 3）输出层

输出层 Y’=H’W2+b2

  • self.predict = torch.nn.Linear(100, n_output)
    1

  • 作用：负责将 100 维隐藏层的输出 映射到 最终的 n_output 维度（通常是 1，表示房价预测值）

  • 仍然是线性变换：Y’=XW2+b2 （其中 W2 和 b2 是可学习参数）

  • 隐藏层 → 输出层 最终输出

    • H 是隐藏层的输出，形状 H'.shape = (N, 100)
    • W2 是 (100, 1) 的权重矩阵 W2.shape = (100, 1)
    • 计算结果 Y 通过 H' × W2，得到 (N, 1) 形状的预测结果: Y′=H′W2

# 4、模型最终产出

  • 最终产出的是经过训练优化后的权重 W1, W2 和偏置 b1, b2
  • 训练的难点是优化这些参数，使损失函数最小化
  • 保存的模型可以用于新数据的预测

# 1）模型本质

  • 主要是权重 W1，W2 和偏置 b1，b2，这些参数用于预测新数据的房价
hidden.weight    torch.Size([100, 13])  # W1
hidden.bias      torch.Size([100])      # b1
output.weight    torch.Size([1, 100])   # W2
output.bias      torch.Size([1])        # b2
1
2
3
4

  • ① (13,100) 的权重矩阵 W1

    • 将 13 维输入特征 映射到 100 维隐藏层
    • 每个隐藏层神经元都有 13 个输入，每个输入都有一个权重，共计 13 * 100 个权重

  • ② (100,1) 的权重矩阵 W2

    • 作用：将 100 维隐藏层 映射到 1 维输出（预测值）
    • 解释：每个输出值由 100 个隐藏层神经元的加权和 计算得到

  • ③ 偏置项 b1 (100,) 和 b2 (1,)

    • 作用：提供额外的自由度，避免输出总是 0

# 2）模型推算过程

训练阶段 和 预测阶段 比较

  • 训练阶段

    • 在训练过程中，我们的目标是调整这些参数，使得损失函数最小化

    • 使用反向传播 计算梯度，优化 W1, W2, b1, b2, 不断更新参数 以减少预测误差

    • W1 = W1 − η⋅∇W1 
W2 = W2 − η⋅∇W2
b1 = b1 − η⋅∇b1
b2 = b2 − η⋅∇b2
      1
      2
      3
      4

  • 预测阶段

    • 在预测阶段，模型已经训练完成，这些参数是固定的，不再更新
    • 输入一个房屋特征向量 X，形状为 (1, 13)
    • 算隐藏层输出 H=ReLU(XW1+b1)
    • 计算最终的房价预测 Y=HW2+b2
  • 参数 训练阶段的作用 预测阶段的作用
    W1 (13, 100) 通过梯度下降不断优化，使得模型学习到更好的特征表示 作为固定参数，直接将输入特征映射到隐藏层
    b1 (100,) 训练过程中调整，优化隐藏层输出 作为固定偏置，保证隐藏层神经元输出的稳定性
    W2 (100, 1) 通过梯度下降优化，使得模型学习到最佳的房价映射方式c 作为固定参数，直接将隐藏层输出转换为房价预测值
    b2 (1,) 训练过程中调整，使模型能更好地拟合数据 作为固定偏置，调整最终预测值

  • 输入特征进行房价预测

    • 在训练阶段，W1, W2, b1, b2 的初始值确实是随机初始化的
    • 但在训练过程中，通过优化算法不断调整这些参数，最终使得模型收敛到一个较优的解
      • 通过 损失函数最小化和 优化算法（如 Adam、SGD） 使参数不断更新，最终模型能有效预测房价
    • 从而保证模型能够学习到期待的 W1, W2, b1, b2

# 02.求偏导细节

# 1、梯度计算

  • 均方误差损失函数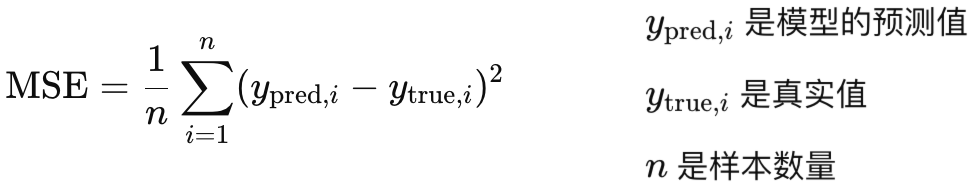

    • 损失函数计算：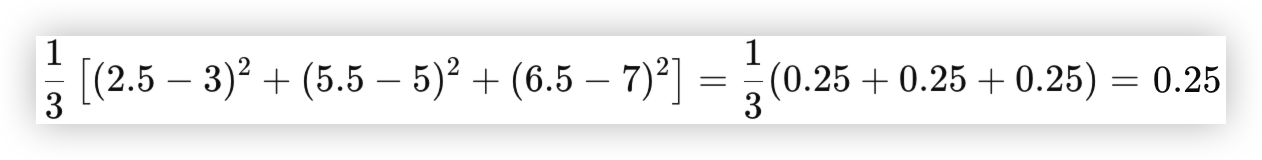

  • 计算 MSELoss 梯度

    • MSELoss 对每个参数的梯度计算 

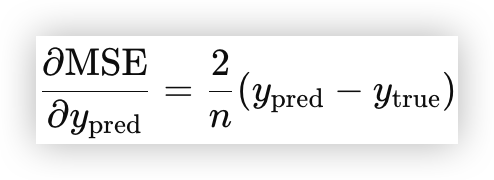
    • import torch
import torch.nn as nn

# 假设真实值和预测值
y_true = torch.tensor([3.0, 5.0, 7.0])
y_pred = torch.tensor([2.5, 5.5, 6.5], requires_grad=True)  # 让 y_pred 可计算梯度

loss_func = nn.MSELoss()       # 定义均方误差损失函数

loss = loss_func(y_pred, y_true)
print("Loss:", loss.item())    # Loss: 0.25 输出损失值

loss.backward()  # 计算梯度
print("Gradient of y_pred:", y_pred.grad)    # 打印 y_pred 的梯度
# [-0.3333,  0.3333, -0.3333]  (2/3 * (2.5-3.0) = -0.3333)
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15

# 2、求偏导图解

上次更新: 2025/3/17 10:59:42
03.神经网络概述
05.手写数字识别

← 05.手写数字识别→

最近更新
01
04.数组双指针排序_子数组
03-25
02
08.动态规划
03-25
03
06.回溯算法
03-25
更多文章>
Theme by Vdoing | Copyright © 2019-2025 逍遥子 技术博客 京ICP备2021005373号