B-tree：节点包含键、指针和数据，磁盘I/O次数较多，适用于内存索引。

B+tree：叶子节点存储数据，内节点只存储键和指针，扇出率高，查询效率高。

MySQL索引实现：InnoDB引擎用B+tree管理索引，根节点常驻内存，树高通常为2-4层。

优化策略：通过节点分裂、延迟合并和缓冲池提高性能。

01.B-tree/B+tree

1、B-Tree

• 在 B-树 中，每个节点通常对应磁盘上的一个块

• 每个磁盘块确实包含键值（keys）、指针（pointers）和数据（data）

• 键值：用于划分节点中的数据范围，帮助决定查找、插入或删除操作时如何导航到正确的子树或叶子节点

• 指针：存储子节点在磁盘上的位置地址，指向子树或叶子节点

• **数据：**存储与键值相关的数据

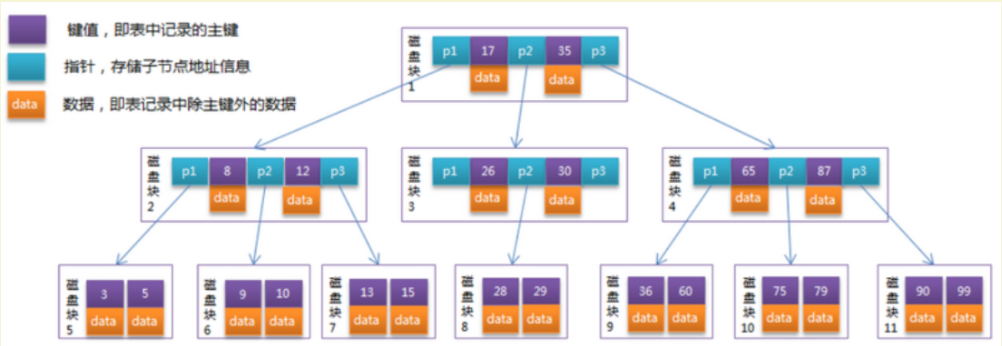
• 模拟查找关键字29的过程

'''模拟查找关键字29的过程：'''
# 根据根节点找到磁盘块1，读入内存【磁盘I/O操作第1次】
# 比较关键字29在区间（17,35），找到磁盘块1的指针P2
# 根据P2指针找到磁盘块3，读入内存【磁盘I/O操作第2次】
# 比较关键字29在区间（26,30），找到磁盘块3的指针P2
# 根据P2指针找到磁盘块8，读入内存【磁盘I/O操作第3次】
# 在磁盘块8中的关键字列表中找到关键字29

2、B+tree

• B-Tree结构图中可以看到每个节点中不仅包含数据的key值，还有data值
• 而每一个页的存储空间是有限的，如果data数据较大时将会导致每个节点（即一个页）能存储的key的数量很小
• 当存储的数据量很大时同样会导致B-Tree的深度较大，增大查询时的磁盘I/O次数，进而影响查询效率

• B+Tree是在B-Tree基础上的一种优化，使其更适合实现外存储索引结构，InnoDB存储引擎就是用B+Tree实现其索引结构
• 在B+Tree中，所有根节点只存储 键和指针，只有叶子节点才存放数据

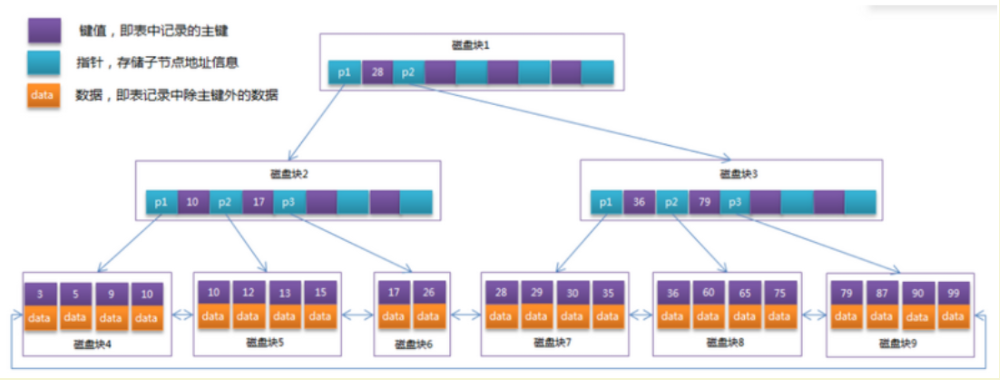
02.B+tree操作

1、查询

• 从根节点开始：

  • 查询操作总是从根节点开始

  • 通过比较查询的键值与当前节点中的关键字，确定进入哪个子树

  • 如果查询的值小于当前节点中的最小键值，则进入最左侧的子树

  • 如果查询的值位于两个键值之间，则进入相应的中间子树

  • 如果查询的值大于当前节点的最大键值，则进入最右侧的子树

• 递归向下搜索：继续递归搜索直到到达叶子节点

• 叶子节点查找：

  • 由于B+树所有数据都存储在叶子节点，查询最终会在叶子节点中进行
  • 若找到目标键值，则返回与之关联的数据；否则，返回"未找到"

• 范围查询：

  • B+树的叶子节点通过链表有序链接，进行范围查询非常高效
  • 只需在找到起始叶子节点后，顺序遍历链接的叶子节点即可

2、插入操作

1）插入

• 插入操作涉及在叶子节点中添加新键值，并在节点满的情况下进行分裂

• 定位叶子节点：首先根据要插入的键值执行与查询类似的操作，找到应插入的叶子节点

• 插入键值：将新键值插入到叶子节点的合适位置，并保持节点内的键值按顺序排列

• 节点分裂：

  • 如果插入后叶子节点的键值数量超过了最大允许数目（即节点满了），则需要进行分裂操作

  • 将叶子节点一分为二，并将中间键值提升到父节点提升的中间键值作为索引指引新的子树范围

  • 如果父节点也满了，则递归进行分裂，可能最终导致树的高度增加

2）节点分裂 推演

• 假设我们有一棵B-树，其阶数（order）为 4，这意味着每个节点最多可以有 3 个键和 4 个子节点

• 1）插入 10, 20, 30

  • 初始时，根节点为空，我们依次插入 10, 20, 30，此时，节点没有超出阶数限制

[10, 20, 30]

• 2）插入 40
  • 插入 40 后，节点超过了阶数 4 的限制（最多只能有 3 个键）
  • 因此，发生节点分裂，中间键 30 被提升到父节点，根节点分裂成两个子节点

         [30]
        /    \
   [10, 20]   [40]

• 3）插入 50, 60
  • 接下来，我们插入 50 和 60，这些键会被插入到右子节点 [40] 中

           [30]
        /       \
   [10, 20]  [40, 50, 60]

• 4）插入 70
  • 插入 70 后，右子节点再次超过了阶数限制，需要进行分裂
  • 中间键 60 被提升到父节点，右子节点分裂为两个子节点
  • 此时，根节点包含 2 个键，未超过限制，继续插入

        [30,   60 ]
        /     |       \
   [10, 20]  [40, 50]  [70]

3、删除操作

1）删除

• 删除操作比插入稍微复杂，需要确保删除后树依然保持平衡
• 如果删除后某个节点中的键值数目低于最小要求，需要进行合并或借用操作

• 定位要删除的键值：与查询过程类似，首先找到要删除的键值所在的叶子节点

• 删除键值：从叶子节点中删除该键值

• 调整结构：

  • 借用关键字：如果删除后叶子节点中的键值数目少于最小要求（通常是阶数的一半），需要从相邻的兄弟节点借用关键字

  • 节点合并：如果借用失败（相邻兄弟节点的关键字数也少于最小要求），则将当前节点与相邻的兄弟节点合并，并删除父节点中的索引关键字

• 递归向上调整：

  • 如果父节点的关键字数目也不满足最小要求，则继续向上调整，直到根节点
  • 若根节点被删除且仅有一个子节点，则子节点成为新的根节点，树的高度减小

2）调整结构 推演

• 假设我们有一棵阶数为 4 的B-树，要求：删除键值 10

           [30]
          /    \
   [10, 20]  [40, 50, 60]

• 1）删除键值 10
  • 删除后，此时左子节点变为 [20]
  • 删除后，该节点中的键值数为 1，低于B-树阶数的一半（(4//2) - 1 = 1），因此需要调整结构

       [30]
      /    \
   [20]  [40, 50, 60]

• 2）借用关键字
  • 会先尝试从相邻的兄弟节点借用关键字
  • 我们检查右兄弟节点 [40, 50, 60]，其键值数为 3，大于最小要求，可以借出一个关键字
    • 从右兄弟节点借用最小的关键字 40，并将 30 替换为借来的 40。
    • 父节点的结构由 [30] 更新为 [40]，左子节点更新为 [20, 30]

        [40]
       /    \
  [20, 30]   [50, 60]

3）节点合并 示例

• 接下来，我们假设删除后的情况无法通过借用关键字来解决，演示如何进行节点合并和递归向上调整

        [50]
       /    \
  [10, 20]   [60]

• 1）删除键值 10

  • 删除后，此时左子节点变为 [20]

  • 删除后，该节点中的键值数为 1，低于B-树阶数的一半（(4//2) - 1 = 1），因此需要调整结构

       [50]
      /   \
   [ 20]   [60]

• 2）借用关键字失败

  • 在这个例子中，右兄弟节点 [60] 只包含一个键，无法借出关键字，因此需要进行节点合并

• 3）节点合并

  • 我们将左子节点 [20] 和右子节点 [60] 合并，同时将父节点中的键 50 放入合并后的节点中
  • 此时，父节点被删除，新的子节点 [20, 50, 60] 成为树的根节点
  • 树的高度减少了一层，形成如下结构

03.MySQL底层索引存储

1、InnoDB存储引擎

• InnoDB存储引擎中页的大小为16KB，一般表的主键类型为INT（占用4个字节）或BIGINT（占用8个字节），指针类型也一般为4或8个字节

• 也就是说一个页（B+Tree中的一个节点）中大概存储16KB/(8B+8B)=1K个键值（这里的K取值为〖10〗^3）

• 也就是说一个深度为3的B+Tree索引可以维护10^3 * 10^3 * 10^3 = 10亿条记录

• 说明：

  • 实际情况中每个节点可能不能填充满，因此在数据库中，B+Tree的高度一般都在2~4层
  • mysql的InnoDB存储引擎在设计时是将根节点常驻内存的，也就是说查找某一键值的行记录时最多只需要1~3次磁盘I/O操作

2、节点分裂与合并

• 在MySQL的InnoDB存储引擎中，确实使用了B+树结构来管理索引

• 因此在数据插入或删除时，可能会出现节点分裂和节点合并的情况

• 然而，MySQL通过多种优化手段，确保这些操作的效率不会显著下降

• 1）节点分裂：

  • 当插入数据导致某个页（B+树的节点）满时，会发生节点分裂
  • 分裂时部分数据会移到新节点，并且父节点会更新指向两个子节点的指针
  • 如果父节点也满了，这个过程会向上递归，最终可能影响根节点

• 2）节点合并：

  • 当删除数据使得某个页中的数据量少于最小阈值时，会触发与相邻节点的合并
  • 同样，这个操作可能向上递归，最终减少树的高度

3、MySQL优化策略

• B+树的扇出率非常高：

  • 由于页的大小为16KB，并且每个页可以存储大约 1K 个键值（如你所计算的）
  • 这意味着一个深度为 3 的B+树可以维护数十亿条记录
  • 实际上，MySQL中的B+树高度通常只有 2~4 层，因此绝大多数查询操作只需 1~3 次磁盘I/O

• 根节点常驻内存：

  • MySQL会将B+树的第一层根节点常驻内存，以减少根节点查找时的磁盘读写操作

• 缓冲池（Buffer Pool）：

  • InnoDB通过缓冲池将数据页和索引页缓存在内存中，以提高读写性能
  • 缓冲池会尽可能缓存常用的页，避免频繁的磁盘加载
  • 当需要对页进行读写时，若该页已经在缓冲池中，操作可以直接在内存中完成，减少磁盘I/O

• 延迟合并：

  • 对于节点合并，InnoDB采用了延迟合并策略，也就是说，删除后并不立即进行节点合并
  • 只有在必要时才执行合并操作，从而减少了频繁的调整
  • eg:
    • 向节点A删除1个键值导致需要进行合并时，InnoDB并不会立即进行合并
    • 如果后续的插入操作向节点A插入了更多键值，节点A就不再需要进行合并
    • 只有在节点A的键值长期低于要求，并且有更多删除或其他触发条件时，InnoDB才会真正执行合并操作

• 批量插入优化：

  • 排序插入：
    • 如果知道要插入的数据是按顺序插入的（例如按照主键顺序）
    • InnoDB可以提前预判插入位置，尽可能减少分裂的发生
  • 批量写入：
    • MySQL可能会通过缓存的方式批量处理这些插入，将数据先写入内存中的缓冲池
    • 然后一次性写入多个键值，避免每次插入都单独触发节点分裂