01. 二叉查找树

1、二叉查找树（BST）

• 要想了解二叉查找树，我们首先看下二叉查找树有哪些特性呢？
• 1， 左子树上所有的节点的值均小于或等于他的根节点的值
• 2， 右子数上所有的节点的值均大于或等于他的根节点的值
• 3， 左右子树也一定分别为二叉排序树

2、二叉树中查找

• 正常的二叉树查找（log(n)）

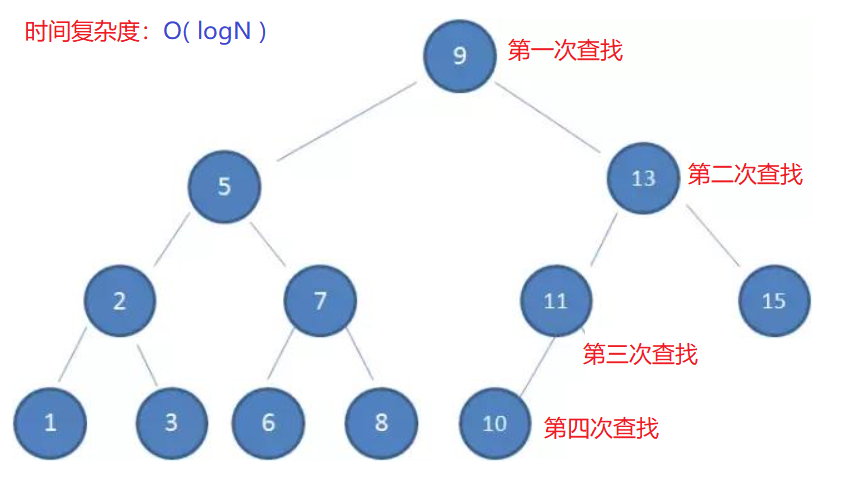
• 二叉查找树有时候也会退化成链表这种形式（时间复杂度：O( N )）

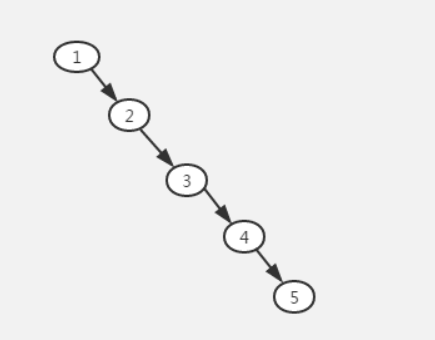
02.红黑树

1、红黑树定义和性质

• 红黑树是一种自平衡的二叉搜索树
• 每个节点额外存储了一个 color 字段 ("RED" or "BLACK")，用于确保树在插入和删除时保持平衡

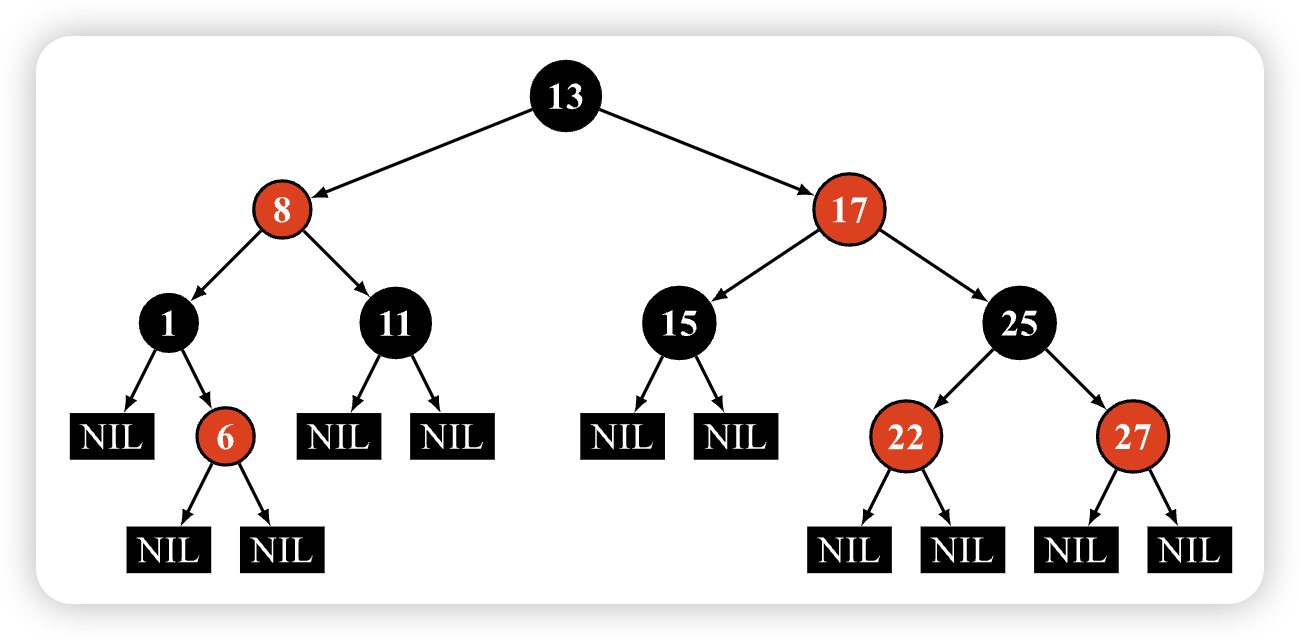
红黑树是一种含有红黑结点并能自平衡的二叉查找树，它必须满足下面性质

• ① 节点为红色或黑色
• ② 根节点为黑色
• ③ NIL 节点（空叶子节点）为黑色
• ④ 红色节点的子节点为黑色
• ⑤ 从根节点到 NIL 节点的每条路径上的黑色节点数量相同

2、左旋、右旋和变色

• 旋转操作是多数平衡树能够维持平衡的关键
• 它能在不改变一棵合法 BST（二叉查找树） 中序遍历结果的情况下改变局部节点的深度

1）左旋

• 以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点
• 右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变

2）右旋

• 以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点
• 左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变

3）变色

• 结点的颜色由红变黑或由黑变红

3、插入操作

• 对于红黑树来说，新插入的节点初始为红色
• 完成插入后需根据插入节点及相关节点的状态进行修正以满足上文提到的四条性质

• 1）该树原先为空，插入第一个节点后不需要进行修正

• 2）当前的节点的父节点为黑色且为根节点，这时性质已经满足，不需要进行修正

• 3）当前节点 N 的父节点 P 是为根节点且为红色，将其染为黑色即可

• 4）当前节点 N 的父节点 P 和叔节点 U均为红色

  • 将 P，U 节点染黑，将 G 节点染红（可以保证每条路径上黑色节点个数不发生改变）

  • 递归维护 G 节点（如果G节点是根节点，强制将G染黑，这样黑色数依然保持一致）

  • 

• 5）当前节点 N 与父节点 P 的方向相反（左子树插入右节点 或 右子树插入左节点）

  • 该种情况无法直接进行维护，需要通过旋转操作将子树结构调整
  • 

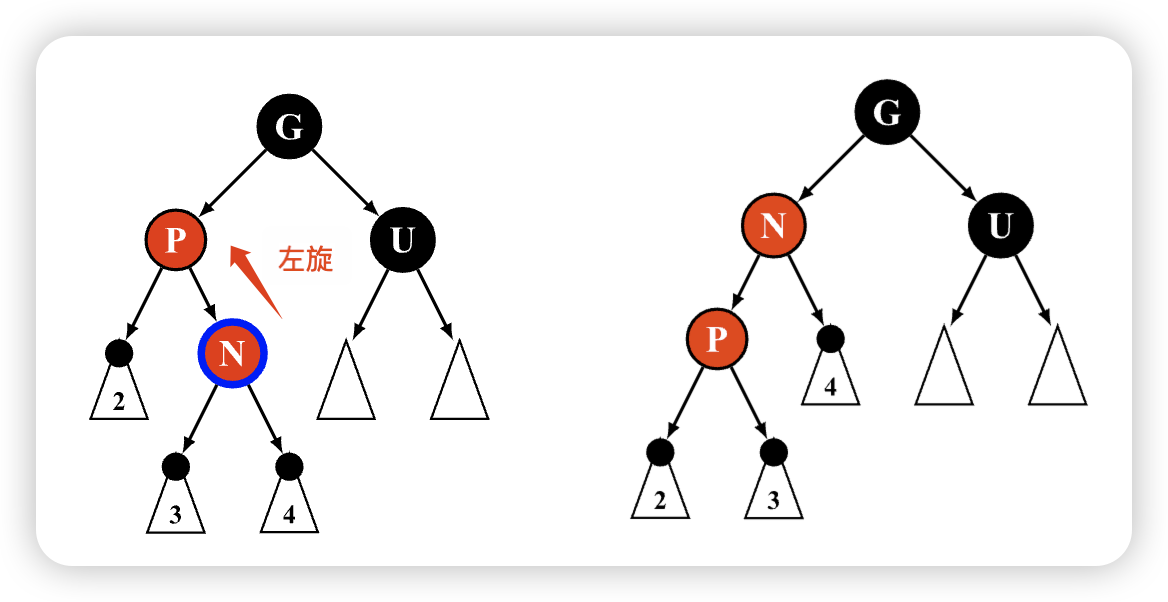
• 6）当前节点 N 与父节点 P 的方向相同（左子树插入左节点 或 右子树插入右节点）

  • 若想在不改变结构的情况下使得子树满足性质 3，则需将 G 染成红色，将 P 染成黑色
  • 这样无法保证路径上黑色数量相同，通过右旋解决
  • 

4、删除操作

• 1）若待删除节点为树中唯一的节点的话，直接删除即可
• 2）若待删除节点 N 既有左子节点又有右子节点
  • 则需找到它的前驱或后继节点进行替换（仅替换数据，不改变节点颜色和内部引用关系）
  • 则后续操作中只需要将后继节点删除即可
• 3）待删除节点为叶子节点
  • 若该节点为红色，直接删除即可
  • 若为黑色，删除后性质 4 被打破，需要重新进行维护